Với giá trị nào của m thì ba đường thẳng phân biệt d1:y=(m+2)x−3m−3;d2:y=x+2 và d3:y=mx+2 giao nhau tại một điểm?
Để 3 đường thẳng trên là ba đường thẳng phân biệt thì {m+2≠1m≠1m≠m+2⇔{m≠1m≠−1
Xét phương trình hoành độ giao điểm của d2 và d3:
x+2=mx+2⇔x(m−1)=0⇔[x=0m=1(ktm)
Với x=0⇒y=2 nên giao điểm của d2,d3 là M(0;2)
Để ba đường thẳng trên giao nhau tại 1 điểm thì M∈d1 . Nên 2=(m+2).0−3m−3⇔3m=−5⇔m=−53(tm)
Vậy m=−53.
Chọn khẳng định đúng về đồ thị hàm số y=ax+b(a≠0).
Đồ thị hàm số y=ax+b(a≠0) là một đường thẳng
Trường hợp 1: Nếu b=0 ta có hàm số y=ax. Đồ thị của y=ax là đường thẳng đi qua gốc tọa độ O(0;0) và điểm A(1;a).
Trường hợp 2: Nếu b≠0 thì đồ thị y=ax+b là đường thẳng đi qua các điểm A(0;b),B(−ba;0).
Trong các hình vẽ sau, hình vẽ nào là đồ thị hàm số y=2x+1
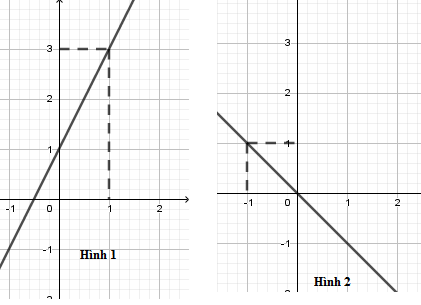
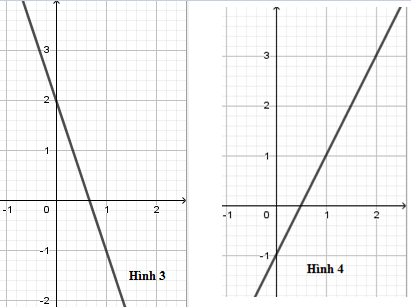
Đồ thị hàm số y=2x+1 là đường thẳng đi qua hai điểm có tọa độ (0;1) và (1;3) nên hình 1 là đồ thị hàm số y=2x+1.
Đồ thị hàm số y=3(x−1)+43 đi qua điểm nào dưới đây?
Thay tọa độ từng điểm vào hàm số ta được
+) Với A(−53;0). Thay x=−53;y=0 vào y=3(x−1)+43 ta được 3(−53−1)+43=0⇔−203=0 (Vô lý)
+) Với B(1;34). Thay x=1;y=34 vào y=3(x−1)+43 ta được 3(1−1)+43=34⇔43=34 (Vô lý)
+) Với D(4;43). Thay x=4;y=43 vào y=3(x−1)+43 ta được 3(4−1)+43=43⇔313=43 (Vô lý)
+)Với C(23;13). Thay x=23;y=13 vào y=3(x−1)+43 ta được 3(23−1)+43=13⇔13=13 (luôn đúng)
⇒C thuộc đồ thị hàm số y=3(x−1)+43
Cho hai đường thẳng d1:y=2x−2 và d2:y=3−4x. Tung độ giao điểm của d1;d2 có tọa độ là
Xét phương trình hoành độ giao điểm của d1 và d2 ta được
2x−2=3−4x⇔6x=5⇔x=56
Thay x=56 vào phương trình đường thẳng d1:y=2x−2 ta được y=2.56−2=−13
Cho đường thẳng d:y=3x−12. Giao điểm của d với trục tung là
Giao điểm của đường thẳng d và trục tung có hoành độ x=0. Thay x=0 vào phương trình y=3x−12 ta được y=3.0−12=−12.
Vậy tọa độ giao điểm cần tìm là D(0;−12)
Cho hàm số y=(1−m)x+m . Xác định m để đồ thị hàm số cắt trục hoành tại điểm có hoành độ x=−3
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ x=−3 nên tọa độ giao điểm là (−3;0).
Thay x=−3;y=0 vào y=(1−m)x+m ta được (1−m).(−3)+m=0
⇔−3+3m+m=0
⇔4m−3=0
⇔4m=3
⇔m=34.
Vậy m=34.
Cho hàm số y=(3−2m)x+m−2 . Xác định m để đồ thị hàm số cắt trục tung tại điểm có tung độ y=−4.
Đồ thị hàm số cắt trục tung tại điểm có tung độ y=−4 nên tọa độ giao điểm là (0;−4)
Thay x=0;y=−4 vào y=(3−2m)x+m−2 ta được (3−2m).0+m−2=−4⇔m=−2.
Vậy m=−2
Cho hàm số y=mx−2 có đồ thị là đường thẳng d1 và hàm số y=12x+1 có đồ thị là đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có hoành độ x=−4.
Ta có phương trình hoành độ giao điểm của d1 và d2:
mx−2=12x+1 (*)
Để hai đường thẳng d1 và d2 cắt nhau tại một điểm có hoành độ x=−4 thì x=−4 thỏa mãn phương trình (*).
Suy ra m.(−4)−2=12.(−4)+1⇔−4m−2=−2+1⇔−4m=1
⇔m=−14.
Cho hàm số y=(m+1)x−1 có đồ thị là đường thẳng d1 và hàm số y=x+1 có đồ thị là đường thẳng d2. Xác định m để hai đường thẳng d1 và d2 cắt nhau tại một điểm có tung độ y=4.
Thay y=4 vào phương trình đường thẳng d2 ta được x+1=4⇔x=3.
Suy ra tọa độ giao điểm của d1 và d2 là (3;4).
Thay x=3;y=4 vào phương trình đường thẳng d1 ta được (m+1).3−1=4⇔m+1=53⇔m=23.
Vậy m=23.
Với giá trị nào của m thì đồ thị hàm số y=−2x+m+2 và y=5x+5−2m cắt nhau tại một điểm trên trục tung?
Để hai đồ thị hàm số y=−2x+m+2 và y=5x+5−2m cắt nhau tại một điểm trên trục tung thì
{−2≠5m+2=5−2m⇔3m=3⇔m=1.
Cho ba đường thẳngd1:y=−2x;d2:y=−3x−1;
d3:y=x+3. Khẳng định nào dưới đây là đúng?
+) Thay tọa độ điểm A(2;1) vào phương trình đường thẳng d1 ta được 1=−2.2⇔1=−4 ( vô lý) nên A∉d1 hay A(2;1) không là giao điểm của d1 và d3. Suy ra A sai.
+) Thay tọa độ điểm B(1;4) vào phương trình đường thẳng d2 ta được 4=−3.1−1⇔4=−4 (vô lý )
Nên B∉d2. Suy ra C sai.
+) Xét tính đồng quy của ba đường thẳng
* Phương trình hoành độ giao điểm của d1 và d2: −2x=−3x−1⇔x=−1⇒y=−2.(−1)⇔y=2
Suy ra tọa độ giao điểm của d1và d2 là \left( { - 1;2} \right).
* Thay x = - 1;y = 2 vào phương trình đường thẳng {d_3} ta được 2 = - 1 + 3 \Leftrightarrow 2 = 2 (luôn đúng)
Vậy ba đường thẳng trên đồng quy tại điểm M\left( { - 1;2} \right).
Với giá trị nào của m thì ba đường thẳng {d_1}:y = x;{d_2}:y = 4 - 3x và {d_3}:y = mx - 3 đồng quy?
Xét phương trình hoành độ giao điểm của {d_1} và {d_2}:
x = 4 - 3x \Leftrightarrow x = 1 \Rightarrow y = 1. Suy ra giao điểm của {d_1} và {d_2} là M\left( {1;1} \right)
Để ba đường thẳng trên đồng quy thì M \in {d_3} nên 1 = m.1 - 3 \Leftrightarrow m = 4.
Vậy m = 4.
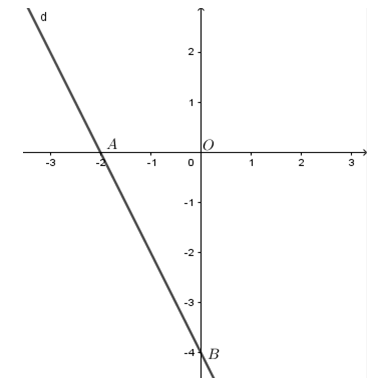
Cho đường thẳng d:y = - 2x - 4 . Gọi A,B lần lượt là giao điểm của d với trục hoành và trục tung. Tính diện tích tam giác OAB.
A\left( {x;0} \right) là giao điểm của d với trục hoành nên 0 = - 2x - 4 \Leftrightarrow x = - 2 \Rightarrow A\left( { - 2;0} \right)
B\left( {0;y} \right) là giao điểm của d với trục tung nên y = - 2.0 - 4 \Leftrightarrow y = - 4 \Rightarrow B\left( {0; - 4} \right).
Suy ra OA = \left| { - 2} \right| = 2;OB = \left| { - 4} \right| = 4.
Vì tam giác OAB vuông tại O nên {S_{OAB}} = \dfrac{{OA.OB}}{2} = \dfrac{{2.4}}{2} = 4 (đvdt)
Cho đường thẳng {d_1}:y = - x + 2 và {d_2}:y = 5 - 4x. Gọi A,B lần lượt là giao điểm của {d_1} với {d_2} và {d_1} với trục hoành. Tổng hoành độ giao điểm của A và B là
+) Phương trình hoành độ giao điểm của {d_1} và {d_2} là - x + 2 = 5 - 4x \Leftrightarrow 3x = 3 \Leftrightarrow x = 1 nên {x_A} = 1
+) B\left( {{x_B};0} \right) là giao điểm của đường thẳng {d_1} và trục hoành. Khi đó ta có 0 = - {x_B} + 2 \Rightarrow {x_B} = 2.
Suy ra tổng hoành độ {x_A} + {x_B} = 1 + 2 = 3.
Gọi {d_1} là đồ thị hàm số y = mx + 1 và {d_2} là đồ thị hàm số y = \dfrac{1}{2}x - 2.
Xác định giá trị của m để M\left( {2; - 1} \right) là giao điểm của {d_1} và {d_2}.
+) Nhận thấy M \in {d_2}.
+) Ta thay tọa độ điểm M vào phương trình {d_1} được phương trình - 1 = 2.m + 1 \Leftrightarrow m = - 1
Vậy m = - 1.
Với giá trị nào của m thì ba đường thẳng {d_1}:y = \left( {m + 2} \right)x - 3;
{d_2}:y = 3x + 1 và {d_3}:y = 2x - 5 giao nhau tại một điểm?
Xét phương trình hoành độ giao điểm của {d_2} và {d_3}:
3x + 1 = 2x - 5 \Leftrightarrow x = - 6 \Rightarrow y = - 17. Suy ra giao điểm của {d_3} và {d_2} là M\left( { - 6; - 17} \right).
Để ba đường thẳng trên đồng quy thì M \in {d_1} nên - 17 = \left( {m + 2} \right).\left( { - 6} \right) - 3 \Leftrightarrow 6\left( {m + 2} \right) = 14 \Leftrightarrow m = \dfrac{1}{3}
Vậy m = \dfrac{1}{3}.
Hình vẽ bên là đồ thị của hàm số nào dưới đây?
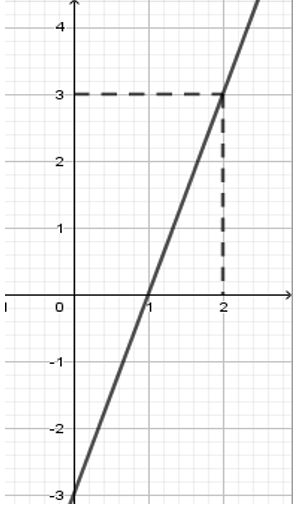
Từ hình vẽ suy ra đồ thị hàm số đi qua hai điểm có tọa độ \left( {1;0} \right) và \left( {2;3} \right) .
Thay tọa độ hai điểm vào mỗi hàm số ta thấy với hàm số y = 3x - 3
+) Thay x = 1;y = 0 và vào hàm số y = 3x - 3 ta được 0 = 3 - 3 \Leftrightarrow 0 = 0 (luôn đúng)
+) Thay x = 2;y = 3 và vào hàm số y = 3x - 3 ta được 3 = 3.2 - 3 \Leftrightarrow 3 = 3 (luôn đúng)
Vậy đồ thị hàm số y = 3x - 3 là đường thẳng như hình vẽ.

