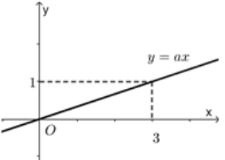
Cho ba đường thẳng\({d_1}:y =  - 2x;{d_2}:y =  - 3x - 1;\)

\({d_3}:y = x + 3.\) Khẳng định nào dưới đây là đúng?

+) Thay tọa độ điểm $A\left( {2;1} \right)$ vào phương trình đường thẳng ${d_1}$ ta được $1 =  - 2.2 \Leftrightarrow 1 =  - 4$ ( vô lý) nên $A \notin {d_1}$ hay $A\left( {2;1} \right)$ không là giao điểm của ${d_1}$ và ${d_3}$. Suy ra A sai.

+) Thay tọa độ điểm $B\left( {1;4} \right)$ vào phương trình đường thẳng  ${d_2}$ ta được $4 =  - 3.1 - 1 \Leftrightarrow 4 =  - 4$ (vô lý )

Nên $B \notin {d_2}$. Suy ra C sai.

+) Xét tính đồng quy của ba đường thẳng

* Phương trình hoành độ giao điểm của ${d_1}$ và ${d_2}$: $ - 2x =  - 3x - 1 \Leftrightarrow x =  - 1$$ \Rightarrow y =  - 2.\left( { - 1} \right) \Leftrightarrow y = 2$

Suy ra tọa độ giao điểm của ${d_1}$và ${d_2}$ là $\left( { - 1;2} \right)$.

* Thay $x =  - 1;y = 2$ vào phương trình đường thẳng ${d_3}$ ta được $2 =  - 1 + 3 \Leftrightarrow 2 = 2$ (luôn đúng)

Vậy ba đường thẳng trên đồng quy tại điểm $M\left( { - 1;2} \right)$.