Phương trình \(\left| {2x + 5} \right| - 3 = x\) có nghiệm là:
\(\begin{array}{l}\;\;\;\;\left| {2x + 5} \right| - 3 = x\\ \Leftrightarrow \left| {2x + 5} \right| = x + 3\,\,\,\left( {x \ge - 3} \right)\\ \Leftrightarrow \left[ \begin{array}{l}2x + 5 = x + 3\\2x + 5 = - \left( {x + 3} \right)\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2\\2x + 5 = - x - 3\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2\\3x = - 8\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = - 2\,(tm)\\x = - \dfrac{8}{3}\,(tm)\end{array} \right.\end{array}\) \(\)
Vậy tập nghiệm của phương trình là S = \(\left\{ { - 2;\dfrac{{ - 8}}{3}} \right\}\).\(\)
Tính nhanh: \(199 + 36 + 201 + 184 + 37\)
Ta có:
\(\begin{array}{l}199 + 36 + 201 + 184 + 37\\ = \left( {199 + 201} \right) + \left( {36 + 184} \right) + 37\\ = 400 + 220 + 37\\ = 620 + 37\\ = 657\end{array}\)
Cho AD là phân giác của \(\Delta ABC\left( {D \in BC} \right)\) có \(AB = 14cm, AC = 21cm, BD = 8cm.\) Độ dài cạnh BC là:
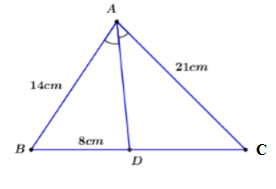
Vì AD là phân giác của tam giác ABC, theo tính chất của đường phân giác ta có:
\(\begin{array}{l}\dfrac{{AB}}{{B{\rm{D}}}} = \dfrac{{AC}}{{C{\rm{D}}}} \Leftrightarrow \dfrac{{14}}{8} = \dfrac{{21}}{{C{\rm{D}}}} \Leftrightarrow C{\rm{D}} = \dfrac{{8.21}}{{14}} = 12cm\\ \Rightarrow BC = B{\rm{D}} + DC = 8 + 12 = 20cm\end{array}\).
Một hình vuông có chu vi \(8000mm\) thì độ dài của cạnh hình vuông là:
Cạnh của hình vuông là: \(8000:4 = 2000mm = 2m\)
Phép trừ \(712,54 - 48,9\) có kết quả đúng là:
Ta có: \(712,54 - 48,9 = 663,64\)
Cho \(\Delta ABC\) và \(MN//BC\) với M nằm giữa A và B, N nằm giữa A và C. Biết \(AN = 2cm, AB = 3AM.\) Kết quả nào sau đây đúng:
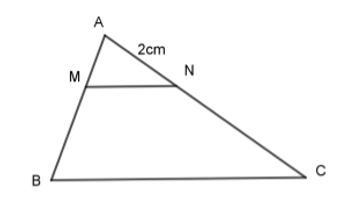
Theo bài ta có: \(AB = 3AM \Rightarrow \dfrac{{AM}}{{AB}} = \dfrac{1}{3}\).
Vì \(MN//BC,\) theo định lý Ta-let ta có:
\(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}} \Leftrightarrow \dfrac{1}{3} = \dfrac{2}{{AC}} \Leftrightarrow AC = 2. 3 = 6cm\).
Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{3}{5}\) và chu vi của \(\Delta A'B'C'\) là $60cm.$ Khi đó chu vi \(\Delta ABC\) là:
Cho \(\Delta ABC\) đồng dạng với \(\Delta A'B'C'\) theo tỉ số \(\dfrac{3}{5}\).
\( \Rightarrow \dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AC}}{{A'C'}} = \dfrac{3}{5}\)\( \Rightarrow \dfrac{{{C_{\Delta ABC}}}}{{{C_{\Delta A'B'C'}}}} = \dfrac{3}{5} \Rightarrow {C_{\Delta ABC}} = \dfrac{3}{5}{C_{\Delta A'B'C'}}.\)
Mà chu vi của tam giác \({C_{\Delta A'B'C'}} = 60cm\) nên \({C_{\Delta ABC}} = \dfrac{3}{5}. 60 = 36cm\).
Một hình hộp chữ nhật có thể tích \(300d{m^3},\) chiều dài \(15dm,\) chiều rộng \(5dm.\) Vậy chiều cao của hình hộp chữ nhật là:
Chiều cao của hình hộp chữ nhật là: \(300:15:5 = 20:5 = 4dm\)
Cho các biểu thức \(A = \dfrac{{2x - 1}}{{x + 3}}\) và \(B = \dfrac{2}{{{x^2} - 9}}\) (với \(x \ne \pm 3\)).
Tìm $x$ để \(A = \dfrac{3}{2}\).
Điều kiện: \(x \ne - 3.\)
\(\begin{array}{l}A = \dfrac{3}{2} \Leftrightarrow \dfrac{{2x - 1}}{{x + 3}} = \dfrac{3}{2}\\ \Rightarrow \left( {2x - 1} \right).2 = 3.\left( {x + 3} \right)\\ \Leftrightarrow 4x - 2 = 3x + 9\\ \Leftrightarrow 4x - 3x = 9 + 2\\ \Leftrightarrow x = 11\;\;\;(tm)\end{array}\).
Vậy \(x = 11\) thì \(A = \dfrac{3}{2}.\)
Cho các biểu thức \(A = \dfrac{{2x - 1}}{{x + 3}}\) và \(B = \dfrac{2}{{{x^2} - 9}}\) (với \(x \ne \pm 3\)).
Tìm \(x\) để \(\dfrac{A}{B} < {x^2} + 5\).
Điều kiện: \(x \ne \pm 3.\)
Ta có: \(\dfrac{A}{B} = \dfrac{{2x - 1}}{{x + 3}}:\dfrac{2}{{{x^2} - 9}} = \dfrac{{2x - 1}}{{x + 3}}.\dfrac{{\left( {x - 3} \right)\left( {x + 3} \right)}}{2} = \dfrac{{\left( {2x - 1} \right)\left( {x - 3} \right)}}{2}.\)
\(\begin{array}{l} \Rightarrow \dfrac{A}{B} < {x^2} + 5 \Leftrightarrow \dfrac{{\left( {2x - 1} \right)\left( {x - 3} \right)}}{2} < {x^2} + 5\\ \Leftrightarrow 2{x^2} - 6x - x + 3 < 2{x^2} + 10\\ \Leftrightarrow 7x > - 7 \Leftrightarrow x > - 1.\end{array}\)
Kết hợp với điều kiện \(x \ne \pm 3\) ta được \(x > - 1\) và \(x \ne 3.\)
Vậy để \(\dfrac{A}{B} < {x^2} + 5\) thì \(x > - 1\) và \(x \ne 3.\)
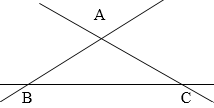
Ở hình vẽ bên có tất cả bao nhiêu điểm, có tất cả bao nhiêu đường thẳng?
Có ba điểm trên hình vẽ là \(A,B,C.\)
Có ba đường thẳng trên hình vẽ là \(AB,AC,BC.\)
Giải bất phương trình \(\dfrac{{x - 1}}{2} + \dfrac{{2 - x}}{3} \le \dfrac{{3x - 3}}{4}\) ta được tập nghiệm là:
\(\begin{array}{l}\;\;\;\dfrac{{x - 1}}{2} + \dfrac{{2 - x}}{3} \le \dfrac{{3x - 3}}{4}\\ \Leftrightarrow \dfrac{{\left( {x - 1} \right).6}}{{2.6}} + \dfrac{{\left( {2 - x} \right).4}}{{3.4}} \le \dfrac{{\left( {3x - 3} \right).3}}{{4.3}}\\ \Leftrightarrow 6\left( {x - 1} \right) + 4\left( {2 - x} \right) \le 3\left( {3x - 3} \right)\\ \Leftrightarrow 6x - 6 + 8 - 4x \le 9x - 9\\ \Leftrightarrow 2x + 2 \le 9x - 9\\ \Leftrightarrow 9x - 2x \ge 2 + 9\\ \Leftrightarrow 7x \ge 11\\ \Leftrightarrow x \ge \dfrac{{11}}{7}\end{array}\)\(\).
Vậy tập nghiệm của bất phương trình là \(S = \left\{ {x|x \ge \dfrac{{11}}{7}} \right\}.\)
Giá trị của biểu thức \(201,5\; - \;36,4:\;2,5\; \times \;0,9\) là:
Ta có
\(\begin{array}{l}201,5\; - \;36,4:\;2,5\; \times \;0,9\\ = 201,5\; - \;14,56\; \times \;0,9\\ = 201,5 - 13,104\\ = 188,396\;\;\end{array}\)
Lúc 6 giờ, ô tô thứ nhất khởi hành từ A. Đến 7 giờ 30 phút ô tô thứ hai cũng khởi hành từ A đuổi theo và kịp gặp ô tô thứ nhất lúc 10 giờ 30 phút. Biết vận tốc ô tô thứ hai lớn hơn vận tốc ô tô thứ nhất là 20km/h. Tính vận tốc ô tô thứ hai?
Gọi vận tốc của ô tô thứ nhất là \(x\;\left( {km/h} \right), \left( {x > 0} \right)\).
\( \Rightarrow \) Vận tốc của ô tô thứ hai là \(x + 20 \left( {km/h} \right)\).
Đổi: 7 giờ 30 phút = 7,5h; 10 giờ 30 phút = 10,5h.
Thời gian ô tô thứ nhất đi đến khi gặp ô tô thứ hai là \(10,5 - 6 = 4,5\;h.\)
Thời gian ô tô thứ hai đi đến khi gặp ô tô thứ nhất là \(10,5 - 7,5 = 3\;h.\)
Theo bài ta có phương trình sau:
\(\begin{array}{l}\;\;\;4,5x = 3\left( {x + 20} \right)\\ \Leftrightarrow 4,5x = 3x + 60\\ \Leftrightarrow 1,5x = 60\\ \Leftrightarrow x = 40\;\left( {tm} \right)\end{array}\)
Vậy vận tốc ô tô thứ nhất là \(40km/h,\) vận tốc ô tô thứ hai là \(40 + 20 = 60\;km/h.\)
Tìm số tự nhiên x, biết rằng: \(814-\left( {x-305} \right) = 712\)
\(\begin{array}{l}814-\left( {x-305} \right) = 712\\x - 305 = 814 - 712\\x - 305 = 102\\x = 102 + 305\\x = 407\end{array}\)
Cho \(\Delta ABC\) vuông tại A, đường cao AH. Kẻ đường phân giác AD của \(\Delta CHA\) và đường phân giác BK của \(\Delta ABC\;(D \in BC;\;K \in AC)\). BK cắt lần lượt AH và AD tại E và F.
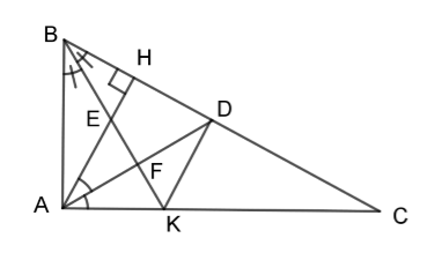
Chọn câu đúng.
Xét \(\Delta AHB\) và \(\Delta CHA\) ta có:
\(\widehat {BHA} = \widehat {AHC} = {90^0}\;\left( {gt} \right)\)
\(\widehat {HAB} = \widehat {HCA}\) (cùng phụ góc \(HAC\))
\( \Rightarrow \Delta AHB \backsim \Delta CHA\; (g - g)\)
Cho \(\Delta ABC\) vuông tại A, đường cao AH. Kẻ đường phân giác AD của \(\Delta CHA\) và đường phân giác BK của \(\Delta ABC\;(D \in BC;\;K \in AC)\). BK cắt lần lượt AH và AD tại E và F.

Chọn câu đúng.
Vì \(\Delta AHB \backsim \Delta CHA\) (chứng minh câu trước) nên \(\widehat {HBA} = \widehat {HAC}\) (cặp góc tương ứng) (1)
Mà theo bài ra ta có:
\(\widehat {HBE} = \dfrac{1}{2}\widehat {HBA}\;\;\;(BK\) là phân giác của \(\widehat {ABC})\;\;\left( 2 \right)\)
\(\widehat {HAD} = \dfrac{1}{2}\widehat {HAC}\;\;(AD\) là phân giác của \(\widehat {HAC})\;\;\left( 3 \right)\)
Từ (1); (2); (3) ta có: \(\widehat {HBE} = \widehat {HAD} = \widehat {EAF}\)
Xét \(\Delta A{\rm{E}}F\) và \(\Delta BEH\) ta có:
\(\widehat {HBE} = \widehat {EAF}\;\;\left( {cmt} \right)\)
\(\widehat {HEB} = \widehat {FEA}\) (2 góc đối đỉnh)
\( \Rightarrow \Delta AEF \backsim \Delta BEH\;\;\left( {g - g} \right)\)
Cho \(\Delta ABC\) vuông tại A, đường cao AH. Kẻ đường phân giác AD của \(\Delta CHA\) và đường phân giác BK của \(\Delta ABC\;(D \in BC;\;K \in AC)\). BK cắt lần lượt AH và AD tại E và F.

Chọn câu đúng nhất?
*) Ta có: \(\Delta AEF \backsim \Delta BEH\) (theo câu trước)
\( \Rightarrow \widehat {AFE} = \widehat {BHE} = {90^0}\) (các góc tương ứng)
\( \Rightarrow BF \bot AD = \left\{ F \right\}.\)
Xét \(\Delta ABD\) ta có: \(BF\) vừa là đường cao đồng thời là đường phân giác của tam giác
\( \Rightarrow \Delta ABD\) là tam giác cân tại \(B \Rightarrow BF\) là đường phân giác của tam giác.
\( \Rightarrow F\) là trung điểm của \(AD\) hay \(AF = FD.\)
Xét \(\Delta AKD\) ta có: \(KF\) vừa là đường cao đồng thời là đường trung tuyến của tam giác
\( \Rightarrow \Delta AKD\) là tam giác cân tại \(K.\)
\( \Rightarrow \widehat {KAD} = \widehat {KDA}\) (hai góc kề đáy)
\( \Rightarrow \widehat {KAD} = \widehat {DAH}\;\left( { = \widehat {KAD}} \right)\)
Mà hai góc này là hai góc so le trong
\( \Rightarrow KD//AH.\)
*) Xét \(\Delta BHA\) và \(\Delta BAC\) ta có:
\(\begin{array}{l}\widehat B:\;chung\\\widehat {BHA} = \widehat {BAC} = {90^0}\;\left( {gt} \right)\\ \Rightarrow \Delta BHA \backsim \Delta BAC\;\left({g - g}\right)\end{array}\)
\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{BA}}{{BC}}\) (các cặp cạnh tương ứng) (*)
Xét \(\Delta BHE\) và \(\Delta BAK\) ta có:
\(\begin{array}{l}\widehat {BHE} = \widehat {BAK} = {90^0}\;\;\left( {gt} \right)\\\widehat {HBE} = \widehat {ABK}\;\;\left( {gt} \right)\\ \Rightarrow \Delta BHE \backsim \Delta BAK\;\;\left( {g - g} \right)\end{array}\)
\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{HE}}{{AK}}\) (các cặp cạnh tương ứng)
Mà \(\Delta AKD\) cân tại \(K\;\;\left( {cm\;c)} \right) \Rightarrow KA = KD\)
\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{HE}}{{AK}} = \dfrac{{EH}}{{KD}}\) (**)
Từ (*) và (**) ta có: \(\dfrac{{EH}}{{KD}} = \dfrac{{BA}}{{BC}}\)\( \Leftrightarrow \dfrac{{EH}}{{AB}} = \dfrac{{KD}}{{BC}}\) (đpcm).
Lớp học có \(18\) nữ và \(12\) nam. Hỏi số học sinh nữ chiếm bao nhiêu phần trăm số học sinh cả lớp?
Số học sinh cả lớp là: \(18 + 12 = 30\) (học sinh)
Số học sinh nữ chiếm số phần trăm so với số học sinh cả lớp là:
\(18:30 \times 100 = 60\left( \% \right)\)
Cho $a,b,c$ là các số thực dương. Chọn câu đúng.
Ta chứng minh bất đẳng thức \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x,y > 0.\)
Ta có \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}} \Leftrightarrow \dfrac{{x + y}}{{xy}} \ge \dfrac{4}{{x + y}}\)\( \Leftrightarrow {\left( {x + y} \right)^2} \ge 4xy \Leftrightarrow {x^2} - 2xy + {y^2} \ge 0\)\( \Leftrightarrow {\left( {x - y} \right)^2} \ge 0\) đúng với mọi \(x,y > 0.\)
Nên ta có \(\dfrac{1}{x} + \dfrac{1}{y} \ge \dfrac{4}{{x + y}}\) với \(x,y > 0.\)
Áp dụng bất đẳng thức trên, ta được:
\(\dfrac{1}{a} + \dfrac{1}{b} \ge \dfrac{4}{{a + b}}\) (1)
\(\dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{4}{{b + c}}\) (2)
\(\dfrac{1}{c} + \dfrac{1}{a} \ge \dfrac{4}{{c + a}}\) (3)
Cộng vế với vế của (1); (2); (3) ta có \(2\left( {\dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c}} \right) \ge 4\left( {\dfrac{1}{{a + b}} + \dfrac{1}{{b + c}} + \dfrac{1}{{c + a}}} \right)\)
\( \Leftrightarrow \dfrac{1}{a} + \dfrac{1}{b} + \dfrac{1}{c} \ge \dfrac{2}{{a + b}} + \dfrac{2}{{b + c}} + \dfrac{2}{{c + a}}\)
Dấu “ = ” xảy ra khi \(a = b = c > 0.\)

