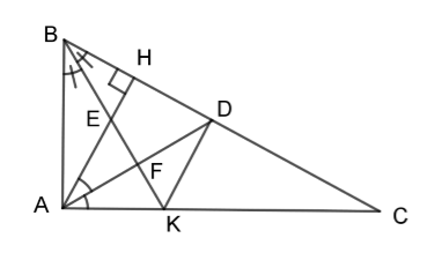
Cho \(\Delta ABC\) vuông tại A, đường cao AH. Kẻ đường phân giác AD của \(\Delta CHA\) và đường phân giác BK của \(\Delta ABC\;(D \in BC;\;K \in AC)\). BK cắt lần lượt AH và AD tại E và F.

Chọn câu đúng nhất?

*) Ta có: \(\Delta AEF \backsim \Delta BEH\) (theo câu  trước)

\( \Rightarrow \widehat {AFE} = \widehat {BHE} = {90^0}\)  (các góc tương ứng)

\( \Rightarrow BF \bot AD = \left\{ F \right\}.\)

Xét \(\Delta ABD\) ta có: \(BF\) vừa là đường cao đồng thời là đường phân giác của tam giác

\( \Rightarrow \Delta ABD\) là tam giác cân tại \(B \Rightarrow BF\) là đường phân giác của tam giác.

\( \Rightarrow F\) là trung điểm của \(AD\) hay \(AF = FD.\)

Xét \(\Delta AKD\) ta có: \(KF\) vừa là đường cao đồng thời là đường trung tuyến của tam giác

\( \Rightarrow \Delta AKD\) là tam giác cân tại \(K.\)

\( \Rightarrow \widehat {KAD} = \widehat {KDA}\)  (hai góc kề đáy)

\( \Rightarrow \widehat {KAD} = \widehat {DAH}\;\left( { = \widehat {KAD}} \right)\)

Mà hai góc này là hai góc so le trong

\( \Rightarrow KD//AH.\) 

*) Xét \(\Delta BHA\) và \(\Delta BAC\) ta có:

\(\begin{array}{l}\widehat B:\;chung\\\widehat {BHA} = \widehat {BAC} = {90^0}\;\left( {gt} \right)\\ \Rightarrow \Delta BHA \backsim \Delta BAC\;\left({g - g}\right)\end{array}\)

\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{BA}}{{BC}}\)  (các cặp cạnh tương ứng)  (*)

Xét \(\Delta BHE\) và \(\Delta BAK\) ta có:

\(\begin{array}{l}\widehat {BHE} = \widehat {BAK} = {90^0}\;\;\left( {gt} \right)\\\widehat {HBE} = \widehat {ABK}\;\;\left( {gt} \right)\\ \Rightarrow \Delta BHE \backsim \Delta BAK\;\;\left( {g - g} \right)\end{array}\)

\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{HE}}{{AK}}\)  (các cặp cạnh tương ứng)

Mà \(\Delta AKD\) cân tại \(K\;\;\left( {cm\;c)} \right) \Rightarrow KA = KD\)

\( \Rightarrow \dfrac{{BH}}{{BA}} = \dfrac{{HE}}{{AK}} = \dfrac{{EH}}{{KD}}\)  (**)

Từ (*) và (**) ta có: \(\dfrac{{EH}}{{KD}} = \dfrac{{BA}}{{BC}}\)\( \Leftrightarrow \dfrac{{EH}}{{AB}} = \dfrac{{KD}}{{BC}}\) (đpcm).