Cho \(\Delta ABC\) vuông tại A, đường cao AH. Kẻ đường phân giác AD của \(\Delta CHA\) và đường phân giác BK của \(\Delta ABC\;(D \in BC;\;K \in AC)\). BK cắt lần lượt AH và AD tại E và F.

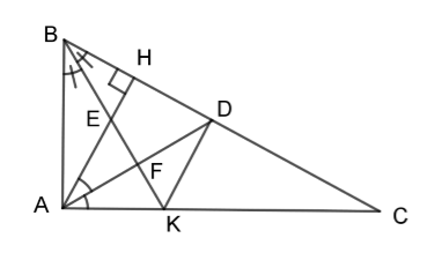
Chọn câu đúng.

Vì \(\Delta AHB \backsim \Delta CHA\) (chứng minh câu trước) nên \(\widehat {HBA} = \widehat {HAC}\) (cặp góc tương ứng)  (1)

Mà theo bài ra ta có:

\(\widehat {HBE} = \dfrac{1}{2}\widehat {HBA}\;\;\;(BK\) là phân giác của \(\widehat {ABC})\;\;\left( 2 \right)\)  

\(\widehat {HAD} = \dfrac{1}{2}\widehat {HAC}\;\;(AD\) là phân giác của \(\widehat {HAC})\;\;\left( 3 \right)\) 

Từ (1); (2); (3) ta có: \(\widehat {HBE} = \widehat {HAD} = \widehat {EAF}\)

Xét \(\Delta A{\rm{E}}F\) và \(\Delta BEH\) ta có:

            \(\widehat {HBE} = \widehat {EAF}\;\;\left( {cmt} \right)\)

            \(\widehat {HEB} = \widehat {FEA}\) (2 góc đối đỉnh)

\( \Rightarrow \Delta AEF \backsim \Delta BEH\;\;\left( {g - g} \right)\)