Nghiệm của phương trình $1 + 7 + 13 + \ldots + x = 280$ là:
Ta thấy tổng $1 + 7 + 13 + \ldots + x$ là tổng của cấp số cộng với \({u_1} = 1,d = 6\).
Giả sử $x$ là số hạng thứ $n$, khi đó \(x = {u_1} + \left( {n - 1} \right)d = 1 + \left( {n - 1} \right)6\), và $\begin{array}{l}1 + 7 + 13 + \ldots + x = \dfrac{{n\left( {2{u_1} + \left( {n - 1} \right)d} \right)}}{2} = \dfrac{{n\left( {2 + \left( {n - 1} \right).6} \right)}}{2} = 280\\ \Rightarrow 2n + 6n\left( {n - 1} \right) = 560\\ \Leftrightarrow 6{n^2} - 4n - 560 = 0 \Leftrightarrow n = 10\end{array}$
Vậy \(x = 1 + 9.6 = 55\).
Cho cấp số cộng \(\left( {{u_n}} \right)\) có công sai d = 2 và \(u_2^2 + u_3^2 + u_4^2\) đạt giá trị nhỏ nhất. Số $2018$ là số hạng thứ bao nhiêu của cấp số cộng \(\left( {{u_n}} \right)\)?
\(\begin{array}{l}u_2^2 + u_3^2 + u_4^2 = {\left( {{u_1} + 2} \right)^2} + {\left( {{u_1} + 4} \right)^2} + {\left( {{u_1} + 6} \right)^2} = 3u_1^2 + 24{u_1} + 56\\ = 3\left( {u_1^2 + 8{u_1}} \right) + 56 = 3{\left( {{u_1} + 4} \right)^2} + 8 \ge 8\end{array}\)
Dấu “=” xảy ra khi và chỉ khi \({u_1} + 4 = 0 \Rightarrow {u_1} = - 4\)
Số hạng tổng quát \({u_n} = {u_1} + \left( {n - 1} \right)d = - 4 + \left( {n - 1} \right).2 = 2n - 6\).
Nếu \({u_n} = 2018 \Rightarrow 2n - 6 = 2018 \Leftrightarrow n = 1012\)
Cho cấp số cộng \(\left( {{x_n}} \right)\) có \({x_3} + {x_{13}} = 80.\) Tính tổng ${S_{15}}$ của $15$ số hạng đầu tiên của cấp số cộng đó?
Ta có \({x_3} + {x_{13}} = 80 \Leftrightarrow {x_1} + 2d + {x_1} + 12d = 80 \Leftrightarrow 2{x_1} + 14d = 80\)
\({S_{15}} = \dfrac{{15\left( {2{x_1} + 14d} \right)}}{2} = \dfrac{{15.80}}{2} = 600\) .
Biết rằng tồn tại các giá trị của \(x \in \left[ {0;2\pi } \right]\) để ba số \(1 + \sin x,\,\,{\sin ^2}x,\,\,1 + \sin 3x\) lập thành một cấp số cộng, tính tổng $S$ các giá trị đó của $x$.
Ta có
$\begin{array}{l}1 + \sin x + 1 + \sin 3x = 2{\sin ^2}x\\ \Leftrightarrow 2 + \sin x + 3\sin x - 4{\sin ^3}x = 2{\sin ^2}x\\ \Leftrightarrow 4{\sin ^3}x + 2{\sin ^2}x - 4\sin x - 2 = 0\\ \Leftrightarrow \left[ \begin{array}{l}\sin x = \pm 1\\\sin x = - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}\cos x = 0\\\sin x = - \dfrac{1}{2}\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{2} + k\pi \\x = - \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{7\pi }}{6} + k2\pi \end{array} \right.\,\,\left( {k \in Z} \right)\\ + )\,\,x = \dfrac{\pi }{2} + k\pi \,\,\left( {k \in Z} \right);\,\,x \in \left[ {0;2\pi } \right] \Rightarrow 0 \le \dfrac{\pi }{2} + k\pi \le 2\pi \\\Leftrightarrow - \dfrac{1}{2} \le k \le \dfrac{3}{2}\mathop \Leftrightarrow \limits^{k \in Z} \left\{ \begin{array}{l}k = 0\\k = 1\end{array} \right. \Rightarrow \left\{ \begin{array}{l}x = \dfrac{\pi }{2}\\x = \dfrac{{3\pi }}{2}\end{array} \right.\\ + )x = - \dfrac{\pi }{6} + k2\pi \,\,\left( {k \in Z} \right);\,\,x \in \left[ {0;2\pi } \right] \Rightarrow 0 \le - \dfrac{\pi }{6} + k2\pi \le 2\pi \\ \Leftrightarrow \dfrac{1}{{12}} \le k \le \dfrac{{13}}{{12}}\mathop \Leftrightarrow \limits^{k \in Z} k = 1 \Rightarrow x = \dfrac{{11\pi }}{6}\\ + )x = \dfrac{{7\pi }}{6} + k2\pi \,\,\left( {k \in Z} \right);\,\,x \in \left[ {0;2\pi } \right] \Rightarrow 0 \le \dfrac{{7\pi }}{6} + k2\pi \le 2\pi \\ \Leftrightarrow \dfrac{{ - 7}}{{12}} \le k \le \dfrac{5}{{12}}\mathop \Leftrightarrow \limits^{k \in Z} k = 0 \Rightarrow x = \dfrac{{7\pi }}{6}\\ \Rightarrow S = \dfrac{\pi }{2} + \dfrac{{3\pi }}{2} + \dfrac{{11\pi }}{{6}} + \dfrac{{7\pi }}{{6}} = 5\pi \end{array}$
Độ dài $3$ cạnh của một tam giác vuông lập thành một cấp số cộng . Nếu trung bình cộng ba cạnh bằng $6$ thì công sai của cấp số cộng này là:
Gọi 3 cạnh của tam giác vuông là \(a,b,c\left( {a < b < c} \right)\). Khi đó ta có hệ phương trình:
\(\begin{array}{l}\left\{ \begin{array}{l}{a^2} + {b^2} = {c^2}\\a + c = 2b\\\dfrac{{a + b + c}}{3} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} = {c^2}\\a + c = 2b\\a + b + c = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{a^2} + {b^2} = {c^2}\\a + c = 2b\\3b = 18\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6\\{a^2} + 36 = {c^2}\\a = 12 - c\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}b = 6\\a = 12 - c\\144 - 24c + {c^2} + 36 = {c^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}b = 6\\c = \dfrac{{15}}{2}\\a = \dfrac{9}{2}\end{array} \right. \\ \Rightarrow d = b - a = 6 - \dfrac{9}{2} = \dfrac{3}{2} = 1,5\end{array}\)
Trên một bàn cờ có nhiều ô vuông. Người ta đặt $7$ hạt dẻ vào ô vuông đầu tiên, sau đó đặt tiếp vào ô vuông thứ hai nhiều hơn ô đầu tiên là $5$ hạt dẻ, tiếp tục đặt vào ô vuông thứ ba số hạt dẻ nhiều hơn ô thứ hai là $5$ hạt dẻ,… và cứ thế tiếp tục đến ô cuối cùng. Biết rằng đặt hết số ô trên bàn cờ người ta phải sử dụng hết $25450$ hạt dẻ. Hỏi bàn cờ đó có bao nhiêu ô?
Gọi ${u_n}$ là số hạt dẻ ở ô thứ $n$ . Khi đó ta có ${u_1} = 7$ và \({u_{n + 1}} = {u_n} + 5,\forall n \ge 1.\)
Dãy số $\left( {{u_n}} \right)$ là cấp số cộng với ${u_1} = 7$ và công sai $d = 5$ nên ta có
\({S_n} = \dfrac{{n\left[ {2{u_1} + \left( {n - 1} \right)d} \right]}}{2} = \dfrac{{n\left[ {2.7 + \left( {n - 1} \right)5} \right]}}{2} = \dfrac{{5{n^2} + 9n}}{2}\)
Theo giả thiết ta có \({S_n} = 25450\) \( \Rightarrow \dfrac{{5{n^2} + 9n}}{2} = 25450 \Leftrightarrow n = 100\)
Vậy bàn cờ có $100$ ô.
Cho cấp số cộng có tổng của $4$ số hạng liên tiếp bằng $22$, tổng bình phương của chúng bằng $166$. Bốn số hạng của cấp số cộng này là:
Gọi 4 số hạng liên tiếp của CSC là \(u,u + d,u + 2d,u + 3d\). Theo giả thiết ta có:
$\begin{array}{l}\left\{ \begin{array}{l}u + u + d + u + 2d + u + 3d = 22\\{u^2} + {\left( {u + d} \right)^2} + {\left( {u + 2d} \right)^2} + {\left( {u + 3d} \right)^2} = 166\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4u + 6d = 22\\4{u^2} + 12ud + 14{d^2} = 166\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}2u + 3d = 11\\2{u^2} + 6ud + 7{d^2} = 83\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}u = \dfrac{{11 - 3d}}{2}\\\dfrac{{9{d^2} - 66d + 121}}{2} + 6\dfrac{{11 - 3d}}{2}d + 7{d^2} = 83\,\,\left( * \right)\end{array} \right.\\\left( * \right) \Leftrightarrow 9{d^2} - 66d + 121 + 66d - 18{d^2} + 14{d^2} = 166\\ \Leftrightarrow 5{d^2} = 45 \Leftrightarrow d = \pm 3\end{array}$
$d = 3 \Rightarrow u = \dfrac{{11 - 3.3}}{2} = 1 \Rightarrow $ 4 số cần tìm là 1, 4, 7, 10
$d = - 3 \Rightarrow u = \dfrac{{11 - 3\left( { - 3} \right)}}{2} = 10 \Rightarrow $ 4 số cần tìm là $10, 7, 4, 1.$
Mặt sàn tầng một của một ngôi nhà cao hơn mặt sân $0,5m$. Cầu thang đi từ tầng một lên tầng hai gồm $21$ bậc, mỗi bậc cao $18cm$. Ký hiệu ${h_n}$ là độ cao của bậc thứ $n$ so với mặt sân. Viết công thức để tìm độ cao ${h_n}$.
Ký hiệu ${h_n}$ là độ cao bậc $n$ so với mặt sân. Khi đó ta có \({h_{n + 1}} = {h_n} + 0,18\,\,\left( m \right)\), trong đó ${h_1} = 0,5 m$ là độ cao của bậc 1 so với mặt sân.
Dãy số \(\left( {{h_n}} \right)\) là cấp số cộng có \({h_1} = 0,5\) và công sai $d = 0,18$. Suy ra số hạng tổng quát của cấp số cộng này là \({h_n} = {h_1} + \left( {n - 1} \right)d= 0,5+ \left( {n - 1} \right)0,18 \)\( = 0,18n + 0,32\) (mét).
Cho ba số dương $a,b,c$ thỏa mãn điều kiện \(\dfrac{1}{{\sqrt b + \sqrt c }},\dfrac{1}{{\sqrt c + \sqrt a }},\dfrac{1}{{\sqrt a + \sqrt b }}\) lập thành một cấp số cộng. Mệnh đề nào dưới đây là đúng ?
Ta có
\(\begin{array}{l}\dfrac{1}{{\sqrt b + \sqrt c }} + \dfrac{1}{{\sqrt a + \sqrt b }} = \dfrac{2}{{\sqrt c + \sqrt a }}\\ \Leftrightarrow \left( {\sqrt c + \sqrt a } \right)\left( {\sqrt a + \sqrt b } \right) + \left( {\sqrt c + \sqrt a } \right)\left( {\sqrt b + \sqrt c } \right) = 2\left( {\sqrt b + \sqrt c } \right)\left( {\sqrt a + \sqrt b } \right)\\ \Leftrightarrow \sqrt {ac} + \sqrt {bc} + a + \sqrt {ab} + \sqrt {bc} + c + \sqrt {ab} + \sqrt {ac} = 2\sqrt {ab} + 2b + 2\sqrt {ac} + 2\sqrt {bc} \\ \Leftrightarrow a + c = 2b\end{array}\)
Khi đó $a,b,c$ lập thành một cấp số cộng.
Tìm tất cả các giá trị của tham số $m$ để phương trình sau có ba nghiệm phân biệt lập thành một cấp số cộng : \({x^3} - 3m{x^2} + 2m\left( {m - 4} \right)x + 9{m^2} - m = 0\) ?
Cách 1: Giải bài toán bằng cách tự luận:
Giả sử phương trình có ba nghiệm phân biệt \({x_1},{x_2},{x_3}\) lập thành một cấp số cộng. Theo định lí Vi-et ta có \({x_1} + {x_2} + {x_3} = - \dfrac{b}{a} = 3m\)
Vì \({x_1},{x_2},{x_3}\) lập thành một cấp số cộng nên \({x_1} + {x_3} = 2{x_2} \Rightarrow {x_1} + {x_2} + {x_3} = 3{x_2} = 3m \Leftrightarrow {x_2} = m\).
Thay ${x_2} = m$ vào phương trình ban đầu ta được \({m^3} - 3{m^3} + 2{m^2}\left( {m - 4} \right) + 9{m^2} - m = {m^2} - m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 1\end{array} \right.\)
Thử lại:
Khi $m = 0$ , phương trình trở thành \({x^3} = 0 \Leftrightarrow x = 0\), phương trình có nghiệm duy nhất (loại)
Khi $m = 1$ , phương trình trở thành \({x^3} - 3{x^2} - 6x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1\\x = 4\end{array} \right.\). Dễ thấy $ - 2,1,4$ lập thành 1 cấp số cộng có công sai $d = 3$.
Vậy $m = 1$ thỏa mãn yêu cầu bài toán.
Cách 2: Giải bài toán bằng cách trắc nghiệm.
Thử lần lượt từng đáp án. Trước hết ta thử đáp án A và D vì $m$ nguyên.
Khi $m = 0$ ta có phương trình \({x^3} = 0 \Leftrightarrow x = 0\), phương trình có nghiệm duy nhất (loại)
Khi $m = 1$ phương trình trở thành \({x^3} - 3{x^2} - 6x + 8 = 0 \Leftrightarrow \left[ \begin{array}{l}x = - 2\\x = 1\\x = 4\end{array} \right.\). Dễ thấy $ - 2,1,4$ lập thành 1 cấp số cộng có công sai $d = 3$ .
Vậy $m = 1$ thỏa mãn yêu cầu bài toán.
Biết rằng tồn tại hai giá trị của tham số $m$ để phương trình sau có bốn nghiệm phân biệt lập thành một cấp số cộng: \({x^4} - 10{x^2} + 2{m^2} + 7m = 0\), tính tổng lập phương của hai giá trị đó.
Đặt \(t = {x^2}\,\,\left( {t \ge 0} \right)\), khi đó phương trình trở thành \({t^2} - 10t + 2{m^2} + 7m = 0\) (*)
Phương trình đã cho có 4 nghiệm dương phân biệt \( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\S > 0\\P > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}25 - 2{m^2} - 7m > 0\\10 > 0\\2{m^2} + 7m > 0\end{array} \right. \Leftrightarrow 0 < 2{m^2} + 7m < 25\)
Với điều kiện trên thì (*) có 2 nghiệm phân biệt dương là \({t_1},{t_2}\,\,\left( {{t_1} < {t_2}} \right)\). Do đó phương trình ban đầu có 4 nghiệm phân biệt được sắp xếp theo thứ tự tăng dần như sau \( - \sqrt {{t_2}} , - \sqrt {{t_1}} ,\sqrt {{t_1}} ,\sqrt {{t_2}} \).
Bốn nghiệm này lập thành cấp số cộng thì \( - \sqrt {{t_1}} + \sqrt {{t_2}} = 2\sqrt {{t_1}} \Leftrightarrow 3\sqrt {{t_1}} = \sqrt {{t_2}} \Leftrightarrow 9{t_1} = {t_2}\)
Mà theo định lí Vi-et ta có \({t_1} + {t_2} = 10 \Leftrightarrow 9{t_2} + {t_2} = 10 \Leftrightarrow {t_2} = 1 \Rightarrow {t_1} = 9\)
Lại có \({t_1}{t_2} = 2{m^2} + 7m = 9 \Leftrightarrow \left[ \begin{array}{l}m = 1\\m = - \dfrac{9}{2}\end{array} \right.\,\,\left( {tm} \right)\)
Do đó \({1^3} + {\left( { - \dfrac{9}{2}} \right)^3} = - \dfrac{{721}}{8}\)
Cho cấp số cộng \(2;5;8;11;14...\) Công sai của cấp số cộng đã cho bằng
\({u_1} = 2;{u_2} = 5\).
Vì đây là cấp số cộng nên công sai \(d = {u_2} - {u_1} = 3\).
Một người làm việc cho một công ty. Theo hợp đồng trong năm đầu tiên, tháng lương thứ nhất là 6 triệu đồng và lương tháng sau cao hơn tháng trước là 200 ngàn đồng. Hỏi theo hợp đồng tháng thứ 7 người đó nhận được lương là bao nhiêu?
Tháng thứ hai người đó nhận được số tiền là: \(6.000.000 + 200.000 = 6.200.000\) đồng.
Tháng thứ ba người đó nhận được số tiền là: \(6.000.000 + 2 \times 200.000 = 6.400.000\) đồng.
Tháng thứ \(n\) người đó nhận được số tiền là: \(6.000.000 + \left( {n - 1} \right) \times 200.000\) đồng.
\( \Rightarrow \) Tháng thứ 7 người đó nhận được số tiền là: \(6.000.000 + 6 \times 200.000 = 7.200.000\) đồng.
Số nghiệm của phương trình $\sin 5 x+\sqrt{3} \cos 5 x=2 \sin 7 x$ trên khoảng $\left(0 ; \dfrac{\pi}{2}\right)$ là
4
4
4
Phương trình
$\Leftrightarrow \dfrac{1}{2} \sin 5 x+\dfrac{\sqrt{3}}{2} \cos 5 x=\sin 7 x\\ \Leftrightarrow \sin \left(5 x+\dfrac{\pi}{3}\right)=\sin 7 x$
$\Leftrightarrow \sin 7 x=\sin \left(5 x+\dfrac{\pi}{3}\right) \Leftrightarrow\left[\begin{array}{l}7 x=5 x+\dfrac{\pi}{3}+k 2 \pi \\ 7 x=\pi-\left(5 x+\dfrac{\pi}{3}\right)+k 2 \pi\end{array} \Leftrightarrow\left[\begin{array}{l}x=\dfrac{\pi}{6}+k \pi \\ x=\dfrac{\pi}{18}+\dfrac{k \pi}{6}\end{array}(k \in \mathbb{Z})\right.\right.$
Xét khoảng $\left(0 ; \dfrac{\pi}{2}\right)$ :
+) $0<\dfrac{\pi}{6}+k \pi<\dfrac{\pi}{2} \Leftrightarrow-\dfrac{1}{6}<k<\dfrac{1}{3} \stackrel{k \in \mathbb{Z}}{\longrightarrow} k=0 \Rightarrow x=\dfrac{\pi}{6}$
+) $0<\dfrac{\pi}{18}+k \dfrac{\pi}{6}<\dfrac{\pi}{2} \Leftrightarrow-\dfrac{1}{3}<k<\dfrac{8}{3} \stackrel{k \in \mathbb{Z}}{\longrightarrow}\left[\begin{array}{l}k=0 \Rightarrow x=\dfrac{\pi}{18} \\ k=1 \Rightarrow x=\dfrac{2 \pi}{9} . \\ k=2 \Rightarrow x=\dfrac{7 \pi}{18}\end{array}\right.$
Vậy phương trình có 4 nghiệm thỏa mãn yêu cầu bài toán
Cho cấp số cộng \(\left( {{u_n}} \right)\) với \({u_1} = 4\), công sai \(d = \dfrac{{48}}{{25}}\). Giá trị của biểu thức:
\(S = \dfrac{1}{{\sqrt {{u_1}} + \sqrt {{u_2}} }} + \dfrac{1}{{\sqrt {{u_2}} + \sqrt {{u_3}} }} + \ldots + \dfrac{1}{{\sqrt {{u_{50}}} + \sqrt {{u_{51}}} }}\) là
\(\dfrac{{25}}{6}\).
\(\dfrac{{25}}{6}\).
\(\dfrac{{25}}{6}\).
Ta có \(S = \dfrac{{\sqrt {{u_2}} - \sqrt {{u_1}} }}{{{u_2} - {u_1}}} + \dfrac{{\sqrt {{u_3}} - \sqrt {{u_2}} }}{{{u_3} - {u_2}}}\)\( + \ldots + \dfrac{{\sqrt {{u_{51}}} - \sqrt {{u_{50}}} }}{{{u_{51}} - {u_{50}}}}\)
\( = \dfrac{{\sqrt {u_{51}} - \sqrt {{u_1}} }}{d}\)\( = \dfrac{{\sqrt {{u_1} + 50d} - \sqrt {{u_1}} }}{d} = \dfrac{{25}}{6}\)
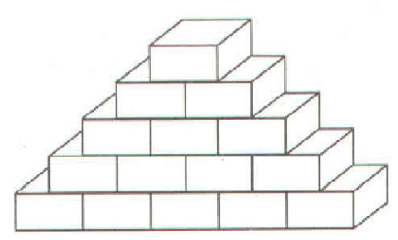
Bà chủ khách sạn trên đèo Mã Pì Lèng muốn trang trí một góc nhỏ trên ban công sân thượng cho đẹp nên quyết định thuê nhân công xây một bức tường gạch với xi măng (như hình vẽ), biết hàng dưới cùng có 500 viên, mỗi hàng tiếp theo đều có ít hơn hàng trước 1 viên và hàng trên cùng có 1 viên. Hỏi số gạch cần dùng để hoàn thành bức tường trên là bao nhiêu viên?
125250
125250
125250
Bước 1: Tìm số hàng.
Theo bài ra ta có số viên gạch từ hàng dưới cùng đến hàng trên cùng lập thành một cấp số cộng với số hạng đầu \({u_1} = 500,d = - 1\).
Công thức tổng quát: \({u_n} = 500 + \left( {n - 1} \right)\left( { - 1} \right) = 501 - n\)
Vì hàng trên cùng có 1 viên nên ta có: \(501 - n = 1 \Leftrightarrow n = 500\)
Bước 2: Tính tổng số viên gạch
Số gạch cần dùng để hoàn thành bức tường trên là \(s = 500 + 499 + 498 + \ldots . + 2 + 1\)\( = \dfrac{{(500 + 1).500}}{2} = 125250\)
Cho một dãy số có các số hạng đầu tiên là \(1,6,16,31,51\). Biết rằng hiệu của hai số hạng liên tiếp của dãy số đó lập thành một cấp số cộng: \(5,10,15,20, \ldots ,5n\). Số 6126 là số hạng thứ bao nhiêu của dãy số đã cho?
\({u_1} = 1;{u_2} = 6;{u_3} = 16;{u_4} = 31.{\rm{ }}\)
\({u_2} - {u_1} = 5.1\)
\({u_3} - {u_1} = 5.2 + 5.1.{\rm{ }}\)
\({u_n} - {u_1} = 5(n - 1) + 5(n - 2) + \ldots + 5.1\)
\( \Rightarrow {u_n} - 1 = 5 \cdot \dfrac{{n(n - 1)}}{2}\)
\( \Rightarrow 6126 - 1 = \dfrac{{5n(n - 1)}}{2} \Rightarrow n = 50\)
\( \Rightarrow 6126\) là số hạng thứ 50 của dãy.

