Các hàm số lượng giác

Đáp án A:

Bước 1:

TXĐ: \(D = \mathbb{R}\).

Bước 2:

Có \(f\left( { - x} \right) = sin\left( { - 2x} \right) + 1 =  - \sin 2x + 1 \ne f\left( x \right)\) nên hàm số này không chẵn không lẻ.

Đáp án B: TXĐ: \(D = \mathbb{R}\).

Có \(f\left( { - x} \right) = \sin \left( { - x} \right).\cos \left( { - 2x} \right) =  - \sin x.\cos 2x =  - f\left( x \right)\) nên hàm số này lẻ.

Đáp án C: TXĐ: \(D = \mathbb{R}\).

Có \(f\left( { - x} \right) = \sin \left( { - x} \right).\sin \left( { - 3x} \right) = \left( { - \sin x} \right).\left( { - \sin 3x} \right) = \sin x.\sin 3x = f\left( x \right)\) nên hàm số này chẵn.

Đáp án D: TXĐ: \(D = \mathbb{R}\).

Có \(f\left( { - x} \right) = \sin \left( { - 2x} \right) + \sin \left( { - x} \right) =  - \sin 2x - \sin x =  - \left( {\sin 2x + \sin x} \right) =  - f\left( x \right)\) nên hàm số này lẻ.

Vậy có hai đáp án đúng là A và C.

Hàm \(y = \sin x\) có TXĐ \(D = R\).

Hàm số \(y = \sin x\) có tập giá trị $\left[ { - 1;1} \right]$.

Hàm số \(y = \cos x\) nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi  + k2\pi } \right)\)

Nếu \(x = 0\) thì \(y = \tan 0 = 0\) nên điểm \(O\) nằm trên đồ thị hàm số \(y = \tan x\)

B sai vì khi thay hoành độ của điểm M vào ta được $y=\tan x=\tan 0=0\ne 1$

C sai vì với $x=\dfrac{\pi}{2}$, không tồn tại $\tan \dfrac{\pi}{2}$

D sai vì với $x=1$ thì ta được $y=\tan 1 \ne 0$

Các hàm số \(y = \sin x,y = \tan x,y = \cot x\) đều là hàm số lẻ.

Hàm số \(y = \cos x\) là hàm số chẵn vì $\cos x = \cos (-x)$

Ta có: $-1 \le \sin \left( {2x - \dfrac{\pi }{4}} \right) \le 1$

\(\begin{array}{l} \Rightarrow \sin \left( {2x - \dfrac{\pi }{4}} \right) \le 1 \\\Leftrightarrow 3.\sin \left( {2x - \dfrac{\pi }{4}} \right) \le 3.1\\ \Rightarrow y=1 + 3\sin \left( {2x - \dfrac{\pi }{4}} \right) \le 1 + 3 = 4\end{array}\)

\(\max y = 4\). Dấu "=" xảy ra khi \(\sin \left( {2x - \dfrac{\pi }{4}} \right)=1\).

Ta có:

\( \sin \left( {2x - \dfrac{\pi }{4}} \right) \ge  - 1\)

\( \Leftrightarrow 3.\sin \left( {2x - \dfrac{\pi }{4}} \right) \ge 3.\left( { - 1} \right)\)

\( \Rightarrow y = 1 + 3\sin \left( {2x - \dfrac{\pi }{4}} \right) \ge 1 + 3.(-1) =  - 2\)

\(\min y =  - 2\). Dấu "=" xảy ra khi \(\sin \left( {2x - \dfrac{\pi }{4}} \right)=-1\).

Vậy \(\max y = 4,\min y =  - 2\)

Hàm số \(y = \sin x\) và \(y = \cos x\) có chu kì \(T = 2\pi \).

Hàm số \(y = \cot x\) và hàm số \(y = \tan x\) có chu kì \(T = \pi \).

Vậy chỉ có đáp án C đúng.

Các hàm số sin, cos đều có đồ thị là đường hình sin nên các đáp án A, B, C đều có đồ thị là đường hình sin.

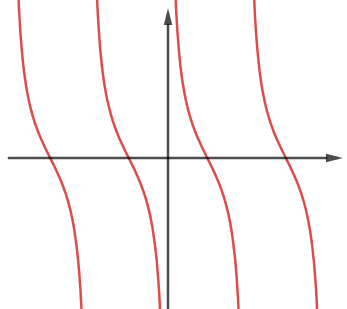
Nhận xét:

Hàm số \(y = \sin x\) và \(y = \cos x\) có đồ thị hình sin nên loại.

Đường cong trên từng đoạn có hướng đi xuống nên hàm số nghịch biến trên mỗi đoạn đó.

Trong các đáp án đã cho thì chỉ có hàm số \(y = \cot x\) có dạng đồ thị như trên.

+) Tìm GTLN

$\begin{array}{l}{\sin ^2}x \ge 0 \Rightarrow 2{\sin ^2}x \ge 0\end{array}$$\Rightarrow 1 + 2{\sin ^2}x \ge 1$

Lấy nghịch đảo 2 vế bất đẳng thức ta được:

$\dfrac{1}{{1 + 2{{\sin }^2}x}} \le \dfrac{1}{1}=1 $

Nhân 2 vế với 4 ta được:

$\Rightarrow \dfrac{4}{{1 + 2{{\sin }^2}x}} \le 4.1 = 4\\\Rightarrow y \le 4$

Dấu “=” xảy ra khi \({\sin ^2}x = 0 \Leftrightarrow\sin x = 0\).

+) Tìm GTNN

$\begin{array}{l}{\sin ^2}x \le 1 \Rightarrow 2{\sin ^2}x \le 2\\\Rightarrow 1 + 2{\sin ^2}x \le 1 + 2 = 3\end{array}$

Lấy nghịch đảo 2 vế bất đẳng thức ta được:

$\dfrac{1}{{1 + 2{{\sin }^2}x}} \ge \dfrac{1}{3}$

Nhân 2 vế với 4 ta được:

$\Rightarrow \dfrac{4}{{1 + 2{{\sin }^2}x}} \ge \dfrac{4}{3}\\\Rightarrow y \ge \dfrac{4}{3}$

Dấu “=” xảy ra khi \({\sin ^2}x= 1\Leftrightarrow\sin x =  \pm 1\).

Vậy GTLN là 4, GTNN là \(\dfrac{4}{3}\).

Bước 1:

Theo công thức hạ bậc ta có: $2{\sin ^2}x=1 - \cos 2x$

=>\(y = 2{\sin ^2}x + {\cos ^2}2x\)\( = 1 - \cos 2x + {\cos ^2}2x\)

\(=(\cos 2x)^2- \cos 2x +1\)

Bước 2:

Đặt \(t = \cos 2x;t \in \left[ { - 1;1} \right]\) ta được \(y = f\left( t \right) = {t^2} - t + 1;t \in \left[ { - 1;1} \right]\).

Bước 3:

Ta cần tìm GTLN và GTNN của hàm số \(f\left( t \right) = {t^2} - t + 1\) trên đoạn \( \in \left[ { - 1;1} \right]\).

\( \Rightarrow f\left( 1 \right) = 1;f\left( {\dfrac{1}{2}} \right) = \dfrac{3}{4};f\left( { - 1} \right) = 3\)

Số lớn nhất là $3$, số nhỏ nhất là \(\dfrac{3}{4}\).

\( \Rightarrow \max y = 3;\min y = \dfrac{3}{4}\).

Điều kiện: \(\cos \left( {2x - \dfrac{\pi }{4}} \right) \ne 0 \Leftrightarrow 2x - \dfrac{\pi }{4} \ne \dfrac{\pi }{2} + k\pi \Leftrightarrow 2x \ne \dfrac{{3\pi }}{4} + k\pi \Leftrightarrow x \ne \dfrac{{3\pi }}{8} + \dfrac{k\pi }{2}\)

Điều kiện: \(\cos 3x - 1 \ne 0 \Leftrightarrow \cos 3x \ne 1 \Leftrightarrow 3x \ne k2\pi  \Leftrightarrow x \ne \dfrac{{k2\pi }}{3}\)

Điều kiện: \(\dfrac{{1 - \cos 3x}}{{1 + \sin 4x}} \ge 0\)

Nhận thấy \(\left\{ \begin{array}{l}\cos 3x \le 1,\forall x \Rightarrow 1 - \cos 3x \ge 0\\\sin 4x \ge  - 1,\forall x \Rightarrow 1 + \sin 4x \ge 0\end{array} \right. \Rightarrow \dfrac{{1 - \cos 3x}}{{1 + \sin 4x}} \ge 0,\forall x\)

Do đó hàm số xác định nếu:

\(1 + \sin 4x \ne 0 \Leftrightarrow \sin 4x \ne  - 1 \Leftrightarrow 4x \ne  - \dfrac{\pi }{2} + k2\pi  \Leftrightarrow x \ne  - \dfrac{\pi }{8} + k\dfrac{\pi }{2}\)

Chu kì của hàm số \(f\left( x \right) = \tan 2x\) là \({T_0} = \dfrac{\pi }{2}\)

Hàm số \(y = \sin 2x\) có chu kì \({T_1} = \dfrac{{2\pi }}{2} = \pi \) và hàm số \(y = \sin x\) có chu kì \({T_2} = 2\pi \).

Vậy chu kì của hàm số \(y = f\left( x \right)\) là \(T = BCNN\left( {{T_1},{T_2}} \right) = 2\pi \).

Đặt \(f\left( x \right) = \tan x.\tan 3x\).

Đáp án A:

\(f\left( {x + 3\pi } \right) = \tan \left( {x + 3\pi } \right).\tan \left[ {3\left( {x + 3\pi } \right)} \right]\) \( = \tan x.\tan \left( {3x + 9\pi } \right) = \tan x.\tan 3x = f\left( x \right)\)

Do đó \(T = 3\pi \) có thể là chu kì của \(f\left( x \right)\).

Đáp án B:

\(f\left( {x + 2\pi } \right) = \tan \left( {x + 2\pi } \right).\tan \left[ {3\left( {x + 2\pi } \right)} \right]\) \( = \tan x.\tan \left( {3x + 6\pi } \right) = \tan x.\tan 3x = f\left( x \right)\)

Do đó \(T = 2\pi \) có thể là chu kì của \(f\left( x \right)\).

Đáp án C:

\(f\left( {x + \dfrac{\pi }{3}} \right) = \tan \left( {x + \dfrac{\pi }{3}} \right).\tan  {3\left( {x + \dfrac{\pi }{3}} \right)} \) \( = \tan \left( {x + \dfrac{\pi }{3}} \right).\tan \left( {3x + \pi } \right) \) \(= \tan \left( {x + \dfrac{\pi }{3}} \right).\tan 3x \ne f\left( x \right)\)

Do đó \(T = \dfrac{\pi }{3}\) không là chu kì của \(f\left( x \right)\).

Đáp án D:

\(f\left( {x + \pi } \right) = \tan \left( {x + \pi } \right).\tan \left[ {3\left( {x + \pi } \right)} \right]\) \( = \tan x.\tan \left( {3x + 3\pi } \right) = \tan x.\tan 3x = f\left( x \right)\)

Do đó \(T = \pi \) có thể là chu kì của \(f\left( x \right)\).

Mà trong ba giá trị \(\pi ,2\pi ,3\pi \) thì \(T = \pi \) là nhỏ nhất nên \(T = \pi \) là chu kì của hàm số đã cho.

TXĐ: \(D = \left[ {0; + \infty } \right)\). Thay lần lượt các đáp án B, C, D vào \(x - T\), nếu \(\exists x \in D:x - T \notin D \) hoặc \(\exists x \in D:x +T \notin D \) thì đáp án không thỏa mãn. Chẳng hạn, ta thử đáp án B: \(T = 2\pi \).

Với \(x = 0 \Rightarrow x - T = - 2\pi \notin D \Rightarrow \) \(\exists x \in D:x - T \notin D \forall T > 0\).

Vậy hàm số không tuần hoàn.

Do \( - 1 \le \sin x \le 1 \Rightarrow -2 \le 2\sin x \le 2 \)\(\Rightarrow -2+3 \le2\sin x + 3 \le 2+3 \)\(\Rightarrow1 \le \sqrt {2\sin x + 3}  \le \sqrt 5 \).

Dấu “=” xảy ra khi lần lượt \(\sin x =  - 1\) và $\sin x = 1$