Ôn tập về giải toán

Ta có hình vẽ:

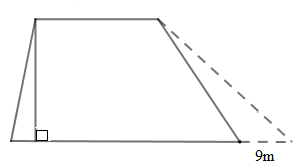
Ta thấy diện tích phần tăng thêm chính là diện tích hình tam giác có đáy $9m$và chiều cao là chiều cao của hình thang.

Diện tích thửa ruộng tăng thêm số mét vuông là:

           $36 \times 9:2 = 162\;({m^2})$

                                      Đáp số: $162{m^2}$.

Tổng độ dài hai đáy là:

            $44 \times 2 = 88\;(m)$

Độ dài đáy lớn của thửa ruộng đó là:

            $(88 + 8):2 = 48\;(m)$

Độ dài đáy bé của thửa ruộng đó là:

            $88 - 48 = 40\;(m)$

Chiều cao của thửa ruộng đó là:

            $48:4 \times 3 = 36\;(m)$

Diện tích thửa ruộng đó là:

            $(48 + 40) \times 36:2 = 1584\;({m^2})$

                                                Đáp số: $1584{m^2}$.

Tổng độ dài hai đáy là:

            $44 \times 2 = 88\;(m)$

Độ dài đáy lớn của thửa ruộng đó là:

            $(88 + 8):2 = 48\;(m)$

Độ dài đáy bé của thửa ruộng đó là:

            $88 - 48 = 40\;(m)$

Chiều cao của thửa ruộng đó là:

            $48:4 \times 3 = 36\;(m)$

Diện tích thửa ruộng đó là:

            $(48 + 40) \times 36:2 = 1584\;({m^2})$

                                                Đáp số: $1584{m^2}$.

Ta có sơ đồ

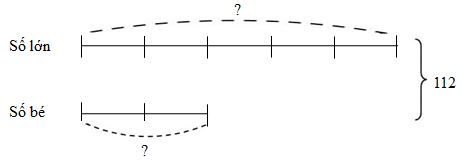
Theo sơ đồ, tổng số phần bằng nhau là:

                   $5 + 2 = 7$ (phần)

Số bé là:

                   $112:7 \times 2 = 32$

Số lớn là:

                   $112 - 32 = 80$

                                    Đáp số: $32\,;\,\,80$.

Số chẵn lớn nhất có hai chữ số là $98$. Vậy hiệu của hai số là $98$.

Ta có sơ đồ:

Theo sơ đồ, hiệu số phần bằng nhau là:

            $3 - 1 = 2$ (phần)

Số lớn là:

            $98:2 \times 3 = 147$

Số bé là:

            $147- 98 = 49$

                                    Đáp số: Số lớn: $147$; số bé: $49$.

Vậy đáp án điền vào ô trống theo thứ tự từ trái sang phải, từ trên xuống dưới là $147\,;\,\,49$.

Nửa chu vi mảnh đất đó là:

            $156:2 = 78\;(m)$

Chiều dài mảnh đất đó là:

            $(78 + 14):2 = 46\;(m)$

Chiều rộng mảnh đất đó là:

            $78 - 46 = 32\;(m)$

Diện tích mảnh đất đó là:

            $46 \times 32 = 1472\;({m^2})$

                                    Đáp số: $1472{m^2}$.

Vậy đáp án đúng điền vào ô trống là $1472$.

$4$ máy bơm : $10$ giờ

$8$ máy bơm : …giờ?

Cách giải:

(Phương pháp rút về đơn vị)

Một máy bơm hút hết số nước ở hồ sau số giờ là:

                  $10 \times 4 = 40$ (giờ)

Nếu dùng $8$ máy bơm thì sẽ hút hết nước ở hồ đó sau số giờ là:

                   $40:8 = 5$ (giờ)

                                 Đáp số: $5$ giờ.

(Phương pháp dùng tỉ số)

$8$ máy bơm gấp $4$ máy  bơm số lần là:

                   $8:4 = 2$ (lần)

Nếu dùng $8$ máy bơm thì sẽ hút hết nước ở hồ đó sau số giờ là:

                  $10:2 = 5$ (giờ)

                                 Đáp số: $5$ giờ.

Tóm tắt:

$8kg$ táo: $120000$ đồng

$15kg$ táo: ..........đồng?

Cách giải:

(Phương pháp rút về đơn vị)

Bác Lan mua $1kg$ táo hết số tiền là:

             $120000:8 = 15000$ (đồng)

Nếu bác mua $15kg$ táo như vậy thì hết số tiền là:

                   $15000 \times 15 = 225000$ (đồng)

                            Đáp số: $225000$ đồng.

(Phương pháp dùng tỉ số)

 $15kg$ táo gấp $8kg$ táo số lần là:

              $15:8 = \dfrac{{15}}{8}$ (lần)

Nếu bác mua $15kg$ táo như vậy thì hết số tiền là:

              $120000 \times \dfrac{{15}}{8} = 225000$ (đồng)

                                       Đáp số: $225000$ đồng.

Đội tuyển học sinh giỏi có tất cả số học sinh là:

                        $18 + 22 = 40$ (bạn)

Tỉ số phần trăm của số học sinh nữ và số học sinh cả đội tuyển là:

                        $\begin{array}{l}22:40 = 0,55\\0,55 = 55\% \end{array}$

                                                Đáp số: $55\%$

Thời gian ô tô đi từ A đến B tính cả thời gian nghỉ là:

            $10$ giờ $- \,6$ giờ $30$ phút $= \,3$ giờ $30$ phút

Thời gian ô tô đi từ A đến B không tính thời gian nghỉ là:

             $3$ giờ $30$ phút $- \,10$ phút $= \,3$ giờ $20$ phút

Đổi $\,3$ giờ $20$ phút $= 3\dfrac{1}{3}$ giờ$= \dfrac{{10}}{3}$ giờ

Vận tốc của ô tô là:

            $168:\dfrac{{10}}{3} = 50,4$ (km/giờ)

                                    Đáp số: $50,4$ km/giờ.

Trong ba ngày, cửa hàng bán được số đường là:

            $4 \times 3 = 12$ (tạ)

Đổi $12$ tạ  $= 1200kg$.

Ngày thứ hai cửa hàng bán được số ki-lô-gam đường là:

            $468:100 \times 75 = 351(kg)$

Ngày thứ ba cửa hàng bán số ki-lô-gam đường là:

            $1200 - (468 + 351) = 381 (kg)$

                                          Đáp số: $381kg$ đường.

Vậy đáp án đúng điền vào ô trống là $381$.

Đổi  $2$ giờ $30$ phút $= \,2,5$ giờ

Vận tốc của ca nô khi đi xuôi dòng là:

            $27,5 + 2,5 = 30$ (km/giờ)

Vận tốc của ca nô khi đi ngược dòng là:

            $27,5 - 2,5 = 25$ (km/giờ)

Độ dài từ bến A đến bến B là:

            $30 \times 2,5 = 75\;(km)$

Ca nô đi ngược dòng khúc sống từ bến B đến bến A hết số thời gian là:

            $75:25 = 3$ (giờ)

                                    Đáp số: $3$ giờ.

Tóm tắt:

$15$ ngày: $16$ người :
$12$ ngày : …người

Số người đến thêm: … người?

Cách giải: (phương pháp rút về đơn vị)

$1$ người ăn hết số gạo đó trong số ngày là:

           $15 \times 16 = 240$ (ngày)

Để ăn hết số gạo đó trong $12$ ngày thì cần số người là:

            $240:12 = 20$ (người)

Số người đến thêm là :

            $20 - 16 = 4$ (người)

                                  Đáp số: $4$ người.

Tổng độ dài hai đáy là:

            $44 \times 2 = 88\;(m)$

Độ dài đáy lớn của thửa ruộng đó là:

            $(88 + 8):2 = 48\;(m)$

Độ dài đáy bé của thửa ruộng đó là:

            $88 - 48 = 40\;(m)$

Chiều cao của thửa ruộng đó là:

            $48:4 \times 3 = 36\;(m)$

Diện tích thửa ruộng đó là:

            $(48 + 40) \times 36:2 = 1584\;({m^2})$

                                                Đáp số: $1584{m^2}$.

Ta có hình vẽ:

Ta thấy diện tích phần tăng thêm chính là diện tích hình tam giác có đáy $9m$và chiều cao là chiều cao của hình thang.

Diện tích thửa ruộng tăng thêm số mét vuông là:

           $36 \times 9:2 = 162\;({m^2})$

                                      Đáp số: $162{m^2}$.

Ta có sơ đồ chuyển động của hai xe:

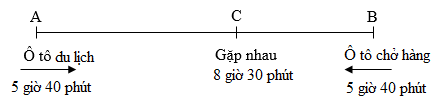
Thời gian đi để hai xe gặp nhau là:

                $8$ giờ $30$ phút $- \,5$ giờ $40$ phút $= 2$ giờ $50$ phút

Đổi $2$ giờ $50$ phút $= \,2\dfrac{5}{6}$ giờ$= \,\dfrac{{17}}{6}$ giờ

Tổng vận tốc của hai xe là:

               $306:\dfrac{{17}}{6} = 108$(km/giờ)

Ta có sơ đồ:

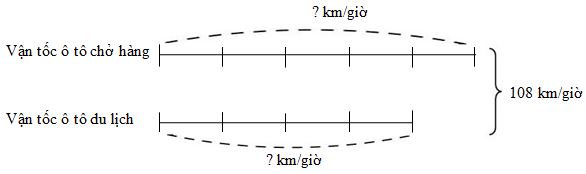
Theo sơ đồ, tổng số phần bằng nhau là:

            $5 + 4 = 9$ (phần)

Vận tốc ô tô chở hàng là:

            $108:9 \times 5 = 60$ (km/giờ)

Vận tốc ô tô du lịch là:

            $108 - 60 = 48$ (km/giờ)

                                 Đáp số: Ô tô du lịch: $48$ km/giờ;

                                              Ô tô chở hàng: $60$ km/giờ.

Vậy đáp án đúng điền vào ô trống theo thứ tự từ trên xuống dưới, từ trái sang phải là $48\,;\,\,60$.

Trong $1$ giờ, cả ba người làm được số phần công việc là:

                        $1:5 = \dfrac{1}{5}$ (công việc)

Trong $1$ giờ,  người thứ nhất làm được số phần công việc là:

                        $1:10 = \dfrac{1}{{10}}$ (công việc)

Trong $1$ giờ, người thứ hai làm được số phần công việc là:

                        $1:6 = \dfrac{1}{6}$ (công việc)

Trong $1$ giờ,  người thứ nhất và người thứ hai làm được số phần công việc là:

                        $\dfrac{1}{{10}} + \dfrac{1}{6} = \dfrac{4}{{15}}$ (công việc)

Trong $1$ giờ,  người thứ ba làm được số phần công việc là:

                        $\dfrac{1}{5} - \dfrac{4}{{15}} = \dfrac{1}{{15}}$ (công việc)

Nếu làm riêng một mình thì người thứ ba làm xong công việc sau số giờ là:

                        $1:\dfrac{1}{{15}} = 15$ (giờ)

                                                Đáp số: $15$ giờ.