Trong các cách viết phân số sau, cách viết nào sai?
\(\dfrac{3}{5};\,\,\dfrac{{18}}{1};\,\,\dfrac{0}{7}\) là các phân số vì có mẫu số khác \(0\).
\(\dfrac{5}{0}\) không là phân số vì có mẫu số bằng \(0\).
.jpg)
Tử số của phân số \(\dfrac{{25}}{{37}}\) là
Trong một phân số, tử số là số tự nhiên viết trên dấu gạch ngang.
Vậy tử số của phân số \(\dfrac{{25}}{{37}}\) là \(25\).
Phân số chỉ số ô vuông đã tô màu trong hình sau là:
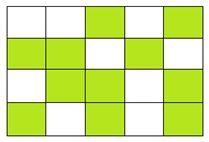
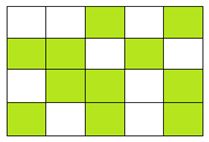
Quan sát hình vẽ ta thấy có tất cả \(20\) ô vuông, trong đó có \(11\) ô vuông được tô màu. Vậy phân số chỉ số ô vuông đã tô màu trong hình là \(\dfrac{{11}}{{20}}\).
Thương của phép chia \(9:14\) được viết dưới dạng phân số là:
Ta có \(9:14 = \dfrac{9}{{14}}\).
Vậy thương của phép chia \(9:14\) được viết dưới dạng phân số là \(\dfrac{9}{{14}}\).
Điền số thích hợp vào chỗ chấm:
\(1 = \dfrac{{...}}{{99}}\)
Ta có: \(1 = \dfrac{{99}}{{99}}\). Vậy số thích hợp điền vào ô trống là \(99\).
.jpg)
Chọn số thích hợp để điền vào chỗ chấm: \(\dfrac{2}{3} = \dfrac{8}{{...}}\)
Ta có : $8:2 = 4$. Nhân cả tử số và mẫu số của phân số \(\dfrac{2}{3}\)với \(4\) ta được
\(\dfrac{2}{3} = \dfrac{{2 \times 4}}{{3 \times 4}} = \dfrac{8}{{12}}\)
Vậy số thích hợp điền vào chỗ chấm là \(12\).
.jpg)
Trong các phân số sau, phân số nào bằng với phân số \(\dfrac{4}{7}\)?
\(\dfrac{8}{{14}}\)
\(\dfrac{{20}}{{35}}\)
\(\dfrac{{52}}{{91}}\)
\(\dfrac{8}{{14}}\)
\(\dfrac{{20}}{{35}}\)
\(\dfrac{{52}}{{91}}\)
\(\dfrac{8}{{14}}\)
\(\dfrac{{20}}{{35}}\)
\(\dfrac{{52}}{{91}}\)
Ta có:
\(\dfrac{4}{7} = \dfrac{{4 \times 2}}{{7 \times 2}} = \dfrac{8}{{14}};\) \(\dfrac{4}{7} = \dfrac{{4 \times 5}}{{7 \times 5}} = \dfrac{{20}}{{35}};\)
\(\dfrac{4}{7} = \dfrac{{4 \times 13}}{{7 \times 13}} = \dfrac{{52}}{{91}}\).
Vậy trong các phân số đã cho, phân số bằng với phân số \(\dfrac{4}{7}\) là \(\dfrac{8}{14};\,\dfrac{{20}}{{35}}; \, \dfrac{{52}}{{91}}\).
Rút gọn phân số \(\dfrac{{15}}{{36}}\) thành phân số tối giản ta được phân số nào sau đây?
Ta có: \(\dfrac{{15}}{{36}} = \dfrac{{15:3}}{{36:3}} = \dfrac{5}{{12}}\).
Vậy rút gọn phân số \(\dfrac{{15}}{{36}}\) ta được phân số tối giản là \(\dfrac{5}{{12}}\).
Chọn số thích hợp để điền vào chỗ chấm: \(\dfrac{{637}}{{741}} = \dfrac{{49}}{{...}}\)
Ta có : $637:49 = 13$. Chia cả tử số và mẫu số của phân số \(\dfrac{{637}}{{741}}\)cho \(13\) ta được
\(\dfrac{{637}}{{741}} = \dfrac{{637:13}}{{741:13}} = \dfrac{{49}}{{57}}\)
Vậy số thích hợp điền vào chỗ chấm là \(57\).
Rút gọn hai phân số \(\dfrac{{91}}{{117}}\) và \(\dfrac{{182}}{{224}}\) thành phân số tối giản, sau đó quy đồng mẫu số ta được hai phân số lần lượt là:
Ta có:
\(\begin{array}{l}\dfrac{{91}}{{117}} = \dfrac{{91:13}}{{117:13}} = \dfrac{7}{9};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{182}}{{224}} = \dfrac{{182:14}}{{224:14}} = \dfrac{{13}}{{16}}\\MSC = 9 \times 16 = 144\\\dfrac{7}{9} = \dfrac{{7 \times 16}}{{9 \times 16}} = \dfrac{{112}}{{144}};\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{13}}{{16}} = \dfrac{{13 \times 9}}{{16 \times 9}} = \dfrac{{117}}{{144}}\,\,\,\,\,\,\,\,\,\,\,\,\,\end{array}\)
Rút gọn hai phân số \(\dfrac{{91}}{{117}}\) và \(\dfrac{{182}}{{224}}\) thành phân số tối giản sau đó quy đồng mẫu số ta được hai phân số lần lượt là \(\dfrac{{112}}{{144}}\)và \(\dfrac{{117}}{{144}}\).
