Cho ΔABC nhọn nội tiếp đường tròn (O). Vẽ phân giác trong AD của góc A (D ≠ (O)). Lấy điểm E thuộc cung nhỏ AC. Nối BE cắt AD và AC lần lượt tại I và tại K, nối DE cắt AC tại J. Kết luận nào đúng?
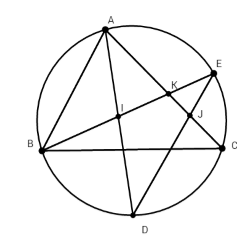
Ta có $\widehat {BID}$ là góc có đỉnh nằm trong đường tròn (O) chắn hai cung BD và AE
$ \Rightarrow \widehat {BID} = \dfrac{1}{2}\left( {s{\rm{đ}}\overparen{BD} + sđ\overparen{AE}} \right)$
+) $\widehat {{\rm{AJ}}E}$ là góc có đỉnh nằm trong đường tròn (O) chắn hai cung CD và AE
\( \Rightarrow \widehat {AJE} = \dfrac{1}{2}(sđ\overparen{AE }+ \)sđ\(\overparen{DC})\)
Mà AD là phân giác của góc A nên sđ$\overparen{BD} = $sđ$\overparen{CD}$
Suy ra $\widehat {BID} = \widehat {{\rm{AJ}}E}$
Cho đường tròn (O). Từ một điểm M nằm ngoài (O), vẽ các cát tuyến MCA và MBD sao cho góc $\widehat {CMD} = {40^0}$. Gọi E là giao điểm của AD và BC. Biết $\widehat {AEB} = {70^0}$, số đo cung lớn AB là
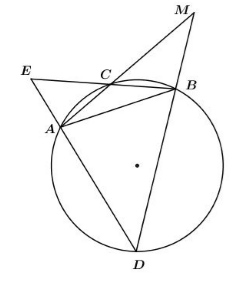
$\begin{array}{l}\widehat {DEB} = \dfrac{1}{2}\left( {sđ\overparen{DB} - sđ\overparen{AC}} \right) = {70^0}\\ \Rightarrow s{\rm{đ}}\overparen{DB} - sđ\overparen{AC} = {140^0}\left( 1 \right)\\\widehat {AMD} = \dfrac{1}{2}\left( {sđ\overparen{AD} - sđ\overparen{BC}} \right) = {40^0}\\ \Rightarrow sđ\overparen{AD} - sđ\overparen{BC} = {80^0}\left( 2 \right)\\sđ\overparen{AC} + sđ\overparen{CB} + sđ\overparen{DB} + sđ\overparen{AD} = {360^0}\left( 3 \right)\\(1) + (2) + (3) \Rightarrow 2\left( {sđ\overparen{DB} + sđ\overparen{AD}} \right) = {580^0}\\ \Leftrightarrow sđ\overparen{DB} + sđ\overparen{AD} = {290^0}\\ \Leftrightarrow sđ\overparen{AB} = {290^0}\end{array}$
Cho tam giác ABC nội tiếp trong đường tròn (O). Trên các cung nhỏ AB và AC lần lượt lấy các điểm I, K sao cho cung AI = cung AK. Dây IK cắt các cạnh AB, AC lân lượt tại D và E.
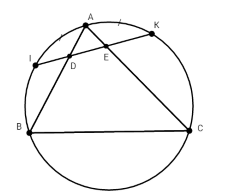
+) Ta có $\widehat {ADK}$ là góc có đỉnh nằm trong đường tròn nên
$\begin{array}{l}\widehat {ADK} = \dfrac{1}{2}\left( {sđ\overparen{AK} + sđ\overparen{IB}} \right) = \dfrac{1}{2}\left( {sđ\overparen{AI} + sđ\overparen{IB}} \right)\\ = \dfrac{1}{2}sđ\overparen{AB} = \widehat {ACB}\end{array}$
+)Ta có $\widehat {ADI}$ là góc có đỉnh nằm trong đường tròn nên
$\begin{array}{l}\widehat {ADI} = \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{IA}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{IA}} \right)\\ = \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{AK}} \right) \\= \dfrac{1}{2}sđ\overparen{AB} = \dfrac{1}{2}\left( {sđ\overparen{AC} + sđ\overparen{CB}} \right)\end{array}$
+)Ta có $\widehat {AEI}$ là góc có đỉnh ở trong đường tròn nên
$\widehat {AEI} = \dfrac{1}{2}\left( {sđ\overparen{AI} + sđ\overparen{KC}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{AK} + sđ\overparen{KC}} \right) = \dfrac{1}{2}sđ\overparen{AC} = \widehat {ABC}$
Cho đường tròn (O) và một dây AB. Vẽ đường kính CD vuông góc với AB (D thuộc cung nhỏ AB). Trên cung nhỏ BC lấy một điểm N. Các đường thẳng CN và DN lần lượt cắt các đường thẳng AB tại E và F. Tiếp tuyến của đường tròn (O) tại N cắt các đường thẳng AB tại I. Chọn đáp án đúng.
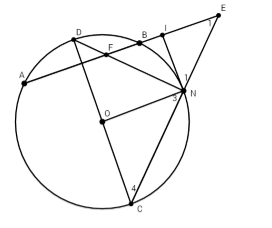
Ta có tam giác AOB cân tại O nên dễ dàng chỉ ra được $sđ\overparen{AD} = sđ\overparen{DB}$
$\begin{array}{l}\widehat {IFN} = \dfrac{1}{2}\left( {sđ\overparen{BN} + sđ\overparen{AD}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{BN} + sđ\overparen{BD}} \right)\\ = \dfrac{1}{2}sđ\overparen{DN} = \widehat {INF}\end{array}$
Suy ra tam giác FIN cân tại I
Ta có:
$\begin{array}{l}{\widehat N_1} + \widehat {{N_3}} = {90^0} \Rightarrow {\widehat N_1} + \widehat {{C_4}} = {90^0}\\\widehat {{E_1}} = \dfrac{1}{2}\left( {sđ\overparen{AC} - sđ\overparen{BN}} \right)\\ = \dfrac{1}{2}\left( {sđ\overparen{BC} - sđ\overparen{CN}} \right) = \dfrac{1}{2}sđ\overparen{NC}\\ \Rightarrow \widehat {{C_4}} + \widehat {{E_1}} = \dfrac{1}{2}sđ\overparen{DN} + \dfrac{1}{2}sđ\overparen{NC} \\= \dfrac{1}{2}sđ\overparen{DC} = {90^0}\\ \Rightarrow \widehat {{E_1}} = \widehat {{N_1}}\end{array}$
Do đó \(\Delta INE\) cân tại I.

