Câu hỏi:
2 năm trước
Cho đường tròn (O). Từ một điểm M nằm ngoài (O), vẽ các cát tuyến MCA và MBD sao cho góc $\widehat {CMD} = {40^0}$. Gọi E là giao điểm của AD và BC. Biết $\widehat {AEB} = {70^0}$, số đo cung lớn AB là
Trả lời bởi giáo viên
Đáp án đúng: c
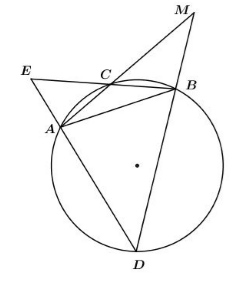
$\begin{array}{l}\widehat {DEB} = \dfrac{1}{2}\left( {sđ\overparen{DB} - sđ\overparen{AC}} \right) = {70^0}\\ \Rightarrow s{\rm{đ}}\overparen{DB} - sđ\overparen{AC} = {140^0}\left( 1 \right)\\\widehat {AMD} = \dfrac{1}{2}\left( {sđ\overparen{AD} - sđ\overparen{BC}} \right) = {40^0}\\ \Rightarrow sđ\overparen{AD} - sđ\overparen{BC} = {80^0}\left( 2 \right)\\sđ\overparen{AC} + sđ\overparen{CB} + sđ\overparen{DB} + sđ\overparen{AD} = {360^0}\left( 3 \right)\\(1) + (2) + (3) \Rightarrow 2\left( {sđ\overparen{DB} + sđ\overparen{AD}} \right) = {580^0}\\ \Leftrightarrow sđ\overparen{DB} + sđ\overparen{AD} = {290^0}\\ \Leftrightarrow sđ\overparen{AB} = {290^0}\end{array}$
Hướng dẫn giải:
+) Nhận biết được góc có đỉnh nằm ngoài đường tròn, góc nội tiếp
+) Tính được số đo góc nằm ngoài đường tròn theo cung bị chắn
+) Nắm vững mối quan hệ góc nội tiếp và số đo cung bị chắn
