Cho tam giác ABC nội tiếp trong đường tròn (O). Trên các cung nhỏ AB và AC lần lượt lấy các điểm I, K sao cho cung AI = cung AK. Dây IK cắt các cạnh AB, AC lân lượt tại D và E.

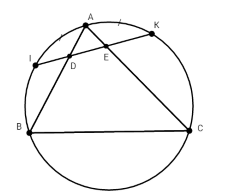
+) Ta có  $\widehat {ADK}$ là góc có đỉnh nằm trong đường tròn nên

$\begin{array}{l}\widehat {ADK} = \dfrac{1}{2}\left( {sđ\overparen{AK} + sđ\overparen{IB}} \right) = \dfrac{1}{2}\left( {sđ\overparen{AI} + sđ\overparen{IB}} \right)\\ = \dfrac{1}{2}sđ\overparen{AB} = \widehat {ACB}\end{array}$

+)Ta có $\widehat {ADI}$ là góc có đỉnh nằm trong đường tròn nên

$\begin{array}{l}\widehat {ADI} = \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{IA}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{IA}} \right)\\ = \dfrac{1}{2}\left( {sđ\overparen{KB} + sđ\overparen{AK}} \right) \\= \dfrac{1}{2}sđ\overparen{AB} = \dfrac{1}{2}\left( {sđ\overparen{AC} + sđ\overparen{CB}} \right)\end{array}$

+)Ta có $\widehat {AEI}$ là góc có đỉnh ở trong đường tròn nên

$\widehat {AEI} = \dfrac{1}{2}\left( {sđ\overparen{AI} + sđ\overparen{KC}} \right) \\= \dfrac{1}{2}\left( {sđ\overparen{AK} + sđ\overparen{KC}} \right) = \dfrac{1}{2}sđ\overparen{AC} = \widehat {ABC}$