Câu hỏi:
2 năm trước
Cho ΔABC nhọn nội tiếp đường tròn (O). Vẽ phân giác trong AD của góc A (D ≠ (O)). Lấy điểm E thuộc cung nhỏ AC. Nối BE cắt AD và AC lần lượt tại I và tại K, nối DE cắt AC tại J. Kết luận nào đúng?
Trả lời bởi giáo viên
Đáp án đúng: a
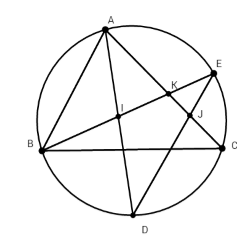
Ta có $\widehat {BID}$ là góc có đỉnh nằm trong đường tròn (O) chắn hai cung BD và AE
$ \Rightarrow \widehat {BID} = \dfrac{1}{2}\left( {s{\rm{đ}}\overparen{BD} + sđ\overparen{AE}} \right)$
+) $\widehat {{\rm{AJ}}E}$ là góc có đỉnh nằm trong đường tròn (O) chắn hai cung CD và AE
\( \Rightarrow \widehat {AJE} = \dfrac{1}{2}(sđ\overparen{AE }+ \)sđ\(\overparen{DC})\)
Mà AD là phân giác của góc A nên sđ$\overparen{BD} = $sđ$\overparen{CD}$
Suy ra $\widehat {BID} = \widehat {{\rm{AJ}}E}$
Hướng dẫn giải:
+) Nhận biết được góc có đỉnh nằm ngoài đường tròn, góc nội tiếp
+) Tính được số đo góc nằm ngoài đường tròn theo cung bị chắn
+) Nắm vững mối quan hệ góc nội tiếp và số đo cung bị chắn
