Một chiếc máy bay đang bay lên với vận tốc $500\,km/h$ . Đường bay lên tạo với phương ngang một góc ${30^0}$. Hỏi sau $1,2$ phút kể từ lúc cất cánh, máy bay đạt được độ cao là bao nhiêu?
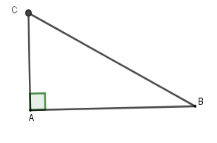
Đổi $1,2' = \dfrac{1}{{50}}h$.
Sau $1,2$ phút máy bay ở $C$.
Quãng đường bay được là $BC = 500.\dfrac{1}{{50}} = 10\,km$ và $\widehat B = 30^\circ $
Nên $AC = BC.\sin 30^\circ = 5\,km$.
Vậy máy bay đạt được độ cao là $5\,km$ sau $1,2$ phút.
Một khúc sông rộng khoảng $250m$. Một chiếc thuyền muốn qua sông theo phương ngang nhưng bị dòng nước đẩy theo phương xiên, nên phải đi khoảng $320m$ mới sang được bờ bên kia. Hỏi dòng nước đã đẩy thuyền lệch đi một góc bao nhiêu độ?
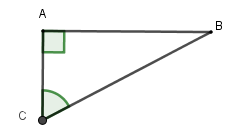
Ta có khúc sông $AC = 250\,m$, quãng đường thuyền đi là $BC = 320\,m$
Góc lệch là $\widehat C$.
Ta có $\cos C = \dfrac{{AC}}{{BC}} = \dfrac{{250}}{{320}} \Rightarrow \widehat C \simeq 38^\circ 37'$
Vậy góc lệch là $38^\circ 37'$.
Hai bạn học sinh Trung và Dũng đang đứng ở mặt đất bằng phẳng, cách nhau $100m$ thì nhìn thấy một chiếc diều ( ở vị trí $C$ giữa hai bạn). Biết góc ''nâng'' để nhìn thấy diều ở vị trí của Trung là ${50^0}$ và góc ''nâng'' để nhìn thấy diều ở vị trí của Dũng là ${40^0}$ . Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
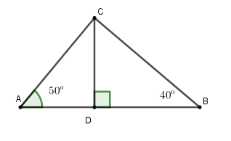
Độ cao của diều là $CD$, độ dài $AB = 100\,m$. Trung đứng ở $A$ , Dũng đứng ở $B$ .
Gọi $AD = x\left( {0 < x < 100} \right)$
$ \Rightarrow BD = 100 - x$
Xét $\Delta ACD$ vuông tại $D$ ta có $CD = AD.\tan A = x.\tan 50^\circ $
Xét $\Delta ABD$ vuông tại $D$ ta có $CD = BD.{\mathop{\rm tanB}\nolimits}$
$ = \left( {100 - x} \right).\tan 40^\circ $
Nên $x.\tan 50^\circ = \left( {100 - x} \right)\tan 40^\circ $
$ \Rightarrow x \simeq 41,32$ (thoả mãn)
$ \Rightarrow CD = 41,32.\tan50^\circ \simeq 49,24\,m$
Vậy độ cao của diều lúc đó so với mặt đất là $49,24\,m$.
Hai bạn học sinh $A$ và $B$ đang đứng ở mặt đất bằng phẳng, cách nhau 80 m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí $C$ nằm trên tia $AB$ và $AC>AB$). Biết góc ''nâng'' để nhìn thấy máy bay ở vị trí của $B$ là \(55^\circ \) góc ''nâng'' để nhìn thấy máy bay ở vị trí của $A$ là $40^\circ $. Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
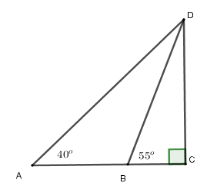
Độ cao của máy bay là $CD$, độ dài $AB=80\,m$.
Gọi $BC = x (x>0)\Rightarrow AC = 80 + x$
Xét tam giác $BDC$ vuông tại $C$ có $CD = x.\tan 55^\circ $
Xét tam giác $ADC$ vuông tại $C$ có $CD = \left( {80 + x} \right).\tan 40^\circ $
Suy ra $x\tan 55^\circ = \left( {80 + x} \right)\tan 40^\circ $
$\Leftrightarrow x \simeq 113,96\,m$
$ \Rightarrow CD = 113,96.\tan 55^\circ $
$\simeq 162,75\,m$
Vậy độ cao của máy bay so với mặt đất là $162,75\,m$.
Bạn Thanh đứng tại vị trí \(A\) cách cây thông \(6m\) và nhìn thấy ngọn của cây này dưới một góc bằng \({55^0}\) so với phương nằm ngang (như hình vẽ). Biết khoảng cách từ mắt của bạn Thanh đến mặt đất bằng \(1,6m.\) Chiều cao \(BC\) của cây thông bằng (làm tròn đến số thập phân thứ hai):
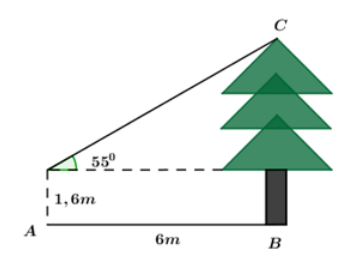
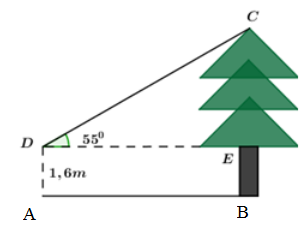Đặt các điểm \(D,\,\,E\) như hình vẽ.
Xét \(\Delta CDE\) vuông tại \(E\) ta có:
\(CE = DE.\tan {55^0} = 6.\tan {55^0} \approx 8,57\,m.\)
\( \Rightarrow \) Chiều cao của cây là: \(BC = CE + BE = 8,57 + 1,6 = 10,17\,\,m.\)
Tính khoảng cách giữa hai điểm \(B\) và \(C,\) biết rằng từ vị trị \(A\) ta đo được \(AB = 234\,m,\,\,\,AC = 185\,m\) và \(\angle BAC = {53^0}\) (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
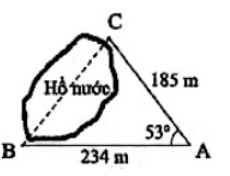
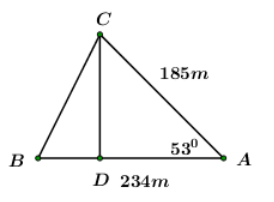
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\)
Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong
\(\Delta ACD\) vuông tại \(D\) ta có:
\(\begin{array}{l}\sin \angle A = \dfrac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\ \Rightarrow CD = 185.\sin {53^0}.\\\cos \angle A = \dfrac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow AD = 185.\cos {53^0}.\\ \Rightarrow BD = AB - AD = 234 - 185.\cos {53^0}.\end{array}\)
Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\)
\(\begin{array}{l}B{C^2} = B{D^2} + C{D^2} = {\left( {234 - 185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {\left( {185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {185^2}\\ \Leftrightarrow B{C^2} \approx 36875,86\\ \Rightarrow BC \approx 192\,m.\end{array}\)
