Câu hỏi:
2 năm trước
Hai bạn học sinh Trung và Dũng đang đứng ở mặt đất bằng phẳng, cách nhau 100m thì nhìn thấy một chiếc diều ( ở vị trí C giữa hai bạn). Biết góc ''nâng'' để nhìn thấy diều ở vị trí của Trung là 500 và góc ''nâng'' để nhìn thấy diều ở vị trí của Dũng là 400 . Hãy tính độ cao của diều lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
Trả lời bởi giáo viên
Đáp án đúng: b
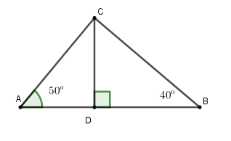
Độ cao của diều là CD, độ dài AB=100m. Trung đứng ở A , Dũng đứng ở B .
Gọi AD=x(0<x<100)
⇒BD=100−x
Xét ΔACD vuông tại D ta có CD=AD.tanA=x.tan50∘
Xét ΔABD vuông tại D ta có CD=BD.tanB
=(100−x).tan40∘
Nên x.tan50∘=(100−x)tan40∘
⇒x≃41,32 (thoả mãn)
⇒CD=41,32.tan50∘≃49,24m
Vậy độ cao của diều lúc đó so với mặt đất là 49,24m.