Câu hỏi:
2 năm trước
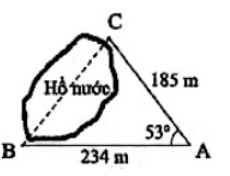
Tính khoảng cách giữa hai điểm \(B\) và \(C,\) biết rằng từ vị trị \(A\) ta đo được \(AB = 234\,m,\,\,\,AC = 185\,m\) và \(\angle BAC = {53^0}\) (kết quả tính bằng mét và làm tròn đến hàng đơn vị).
Trả lời bởi giáo viên
Đáp án đúng: c
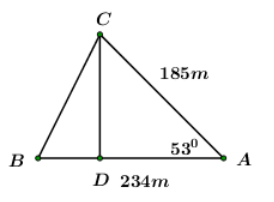
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\)
Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong
\(\Delta ACD\) vuông tại \(D\) ta có:
\(\begin{array}{l}\sin \angle A = \dfrac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\ \Rightarrow CD = 185.\sin {53^0}.\\\cos \angle A = \dfrac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow AD = 185.\cos {53^0}.\\ \Rightarrow BD = AB - AD = 234 - 185.\cos {53^0}.\end{array}\)
Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\)
\(\begin{array}{l}B{C^2} = B{D^2} + C{D^2} = {\left( {234 - 185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {\left( {185.\cos {{53}^0}} \right)^2} + {\left( {185.\sin {{53}^0}} \right)^2}\\ \Leftrightarrow B{C^2} = {234^2} - 2.234.185\cos {53^0} + {185^2}\\ \Leftrightarrow B{C^2} \approx 36875,86\\ \Rightarrow BC \approx 192\,m.\end{array}\)
Hướng dẫn giải:
Từ \(C,\) dựng đường vuông góc với \(AB,\) cắt \(AB\) tại \(D.\)
Khi đó ta có: \(CD\) là đường cao của \(\Delta ABC.\)
Áp dụng tỉ số lượng giác của góc nhọn trong
\(\Delta ACD\) vuông tại \(D\) ta có:
\(\begin{array}{l}\sin \angle A = \dfrac{{CD}}{{CA}} \Rightarrow CD = CA.\sin \angle A\\\cos \angle A = \dfrac{{AD}}{{AC}} \Rightarrow AD = CA.\cos \angle A\\ \Rightarrow BD = AB - AD.\end{array}\)
Áp dụng định lý Pitago cho \(\Delta BCD\) để tính \(BC.\)
Câu hỏi khác
- Bài tập một số hệ thức về cạnh và đường cao trong tam giác vuông toán 9 có lời giải
- Bài tập một số hệ thức về cạnh và góc trong tam giác vuông toán 9 có lời giải
- Bài tập tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập ứng dụng thực tế tỉ số lượng giác của góc nhọn toán 9 có lời giải
- Bài tập hay và khó chương hệ thức lượng trong tam giác vuông toán 9 có lời giải
