Hai bạn học sinh $A$ và $B$ đang đứng ở mặt đất bằng phẳng, cách nhau 80 m thì nhìn thấy một máy bay trực thăng điều khiển từ xa (ở vị trí $C$ nằm trên tia $AB$ và $AC>AB$). Biết góc ''nâng'' để nhìn thấy máy bay ở vị trí của $B$ là \(55^\circ \) góc ''nâng'' để nhìn thấy máy bay ở vị trí của $A$ là $40^\circ $. Hãy tính độ cao của máy bay lúc đó so với mặt đất? (làm tròn đến chữ số thập phân thứ hai)
Trả lời bởi giáo viên
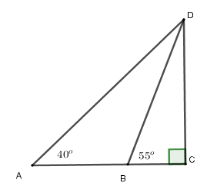
Độ cao của máy bay là $CD$, độ dài $AB=80\,m$.
Gọi $BC = x (x>0)\Rightarrow AC = 80 + x$
Xét tam giác $BDC$ vuông tại $C$ có $CD = x.\tan 55^\circ $
Xét tam giác $ADC$ vuông tại $C$ có $CD = \left( {80 + x} \right).\tan 40^\circ $
Suy ra $x\tan 55^\circ = \left( {80 + x} \right)\tan 40^\circ $
$\Leftrightarrow x \simeq 113,96\,m$
$ \Rightarrow CD = 113,96.\tan 55^\circ $
$\simeq 162,75\,m$
Vậy độ cao của máy bay so với mặt đất là $162,75\,m$.