Bất phương trình

Ta có $-{x^2} + 6x + 7\; = 0 \Leftrightarrow \left[ \begin{array}{l}x = 7\\x =  - 1\end{array} \right.$.

Bảng xét dấu

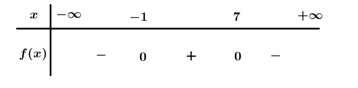
Dựa vào bảng xét dấu $-{x^2} + 6x + 7\; \ge 0 \Leftrightarrow  - 1 \le x \le 7.$

Bất phương trình $5x - 1 \ge \dfrac{{2x}}{5} + 3$$\Leftrightarrow 25x - 5 \ge 2x + 15 \Leftrightarrow 23x \ge 20 \Leftrightarrow x \ge \dfrac{{20}}{{23}}.$

 Ta có $-2{x^2} + 3x - 7\; = 0$ vô nghiệm.

Bảng xét dấu

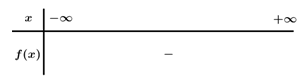
Dựa vào bảng xét dấu $- 2{x^2} + 3x - 7 \ge 0\, \Leftrightarrow \,x \in \emptyset$.

Ta có $f\left( x \right) = {x^2} - 8x + 7 = 0\, \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 7\end{array} \right.$.

Bảng xét dấu

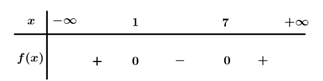
Dựa vào bảng xét dấu $f\left( x \right) \ge 0\, \Leftrightarrow \,\left[ \begin{array}{l}x \le 1\\x \ge 7\end{array} \right.$.

Tập nghiệm của bất phương trình là $S = \left( { - \infty ;1} \right] \cup \,\left[ {7; + \infty } \right)$.

Vì $\dfrac{{13}}{2} \in \left[ {6; + \infty } \right)$ và $\dfrac{{13}}{2} \notin S$ nên $\left[ {6; + \infty } \right)$ thỏa yêu cầu bài toán.

Ta có $f\left( x \right) = 0 \Leftrightarrow \left( {x + 5} \right)\left( {3 - x} \right) = 0.$

Phương trình $x + 5 = 0 \Leftrightarrow x =  - \,5$ và $3 - x = 0 \Leftrightarrow x = 3.$

Bảng xét dấu:

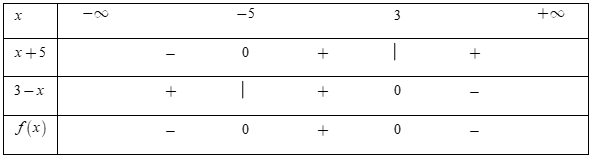
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \le 0 \Leftrightarrow x \in \left( { - \,\infty ; - \,5} \right] \cup \left[ {3; + \,\infty } \right).$

Bất phương trình $x\left( {2 - x} \right) \ge x\left( {7 - x} \right) - 6\left( {x - 1} \right)$

$\Leftrightarrow 2x - {x^2} \ge 7x - {x^2} - 6x + 6 \Leftrightarrow x \ge 6$.

Mà $x \in \mathbb{Z};x \in \left[ { - 10;10} \right] \Rightarrow x \in \left\{ {6;7;8;9;10} \right\}$

Vậy tổng các nghiệm nguyên cần tìm là: 6+7+8+9+10=40.

Bất phương trình $x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right) \Leftrightarrow {x^2} + 5x \le 2{x^2} + 4 \Leftrightarrow {x^2} - 5x + 4 \ge 0$

Xét phương trình ${x^2} - 5x + 4 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right..$

Lập bảng xét dấu:

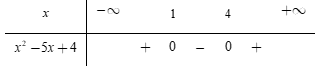
Dựa vào bảng xét dấu, ta thấy nghiệm của bất phương trình ${x^2} - 5x + 4 \ge 0$ là $x \in \left( { - \,\infty ;1} \right] \cup \left[ {4; + \,\infty } \right).$

Ta có $f\left( x \right) \le 0 \Leftrightarrow \dfrac{1}{{3x - 6}} \le 0 \Leftrightarrow 3x - 6 < 0 \Leftrightarrow x < 2 \Leftrightarrow x \in \left( { - \,\infty ;2} \right).$

Điều kiện: $x > 4.$

Bất phương trình tương đương :

$x - 2 \le 4 \Leftrightarrow x \le 6 \Rightarrow 4 < x \le 6$

Mà $x \in \mathbb{Z} \Rightarrow x = 5;x = 6 \Rightarrow S = 5 + 6 = 11$

Đặt $f\left( x \right) = {x^2}\left( {x - 2} \right).$

Phương trình ${x^2} = 0 \Leftrightarrow x = 0$ và $x - 2 = 0 \Leftrightarrow x = 2.$

Lập bảng xét dấu

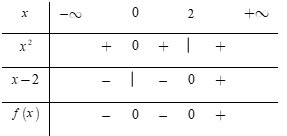
Dựa vào bảng xét dấu ta thấy:

+) Đáp án A: $x - 2 \le 0 \Leftrightarrow x \le 2$ và ${x^2}\left( {x - 2} \right) \le 0 \Leftrightarrow x \le 2$ nên hai bất phương trình tương đương. Chọn A.

+) Đáp án B: $x - 2 < 0 \Leftrightarrow x < 2$ và ${x^2}\left( {x - 2} \right) > 0 \Leftrightarrow x > 2$ nên hai bất phương trình không tương đương. Loại B.

+) Đáp án C: $x - 2 < 0 \Leftrightarrow x < 2$ và ${x^2}\left( {x - 2} \right) < 0 \Leftrightarrow \left\{ \begin{array}{l}x < 2\\x \ne 0\end{array} \right.$ nên hai bất phương trình không tương đương. Loại C.

+) Đáp án D: ${x^2}\left( {x - 2} \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x \ge 2\end{array} \right.$ và $x - 2 \ge 0 \Leftrightarrow x \ge 2$ nên hai bất phương trình không tương đương. Loại D.

- Phương trình $x + 3 = 0 \Leftrightarrow x =  - \,3;\,\,2 - x = 0 \Leftrightarrow x = 2$ và $x - 1 = 0 \Leftrightarrow x = 1.$

- Bảng xét dấu

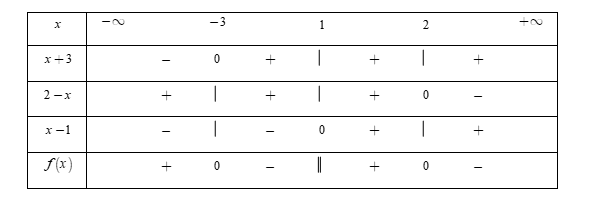
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) > 0 \Leftrightarrow x \in \left( { - \,\infty ; - \,3} \right) \cup \left( {1;2} \right).$

- Vì $2{x^2} - 3x + 2 > 0\,\,\forall x \in \mathbb{R}$ nên:

- Bất phương trình $- 1 \le \dfrac{{{x^2} + 5x + m}}{{2{x^2} - 3x + 2}} < 7$ có tập nghiệm là $\mathbb{R}$ khi hệ sau có tập nghiệm là $\mathbb{R}$:

 $\left\{ \begin{array}{l} - 1\left( {2{x^2} - 3x + 2} \right) \le {x^2} + 5x + m\\{x^2} + 5x + m < 7\left( {2{x^2} - 3x + 2} \right)\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}13{x^2} - 26x + 14 - m > 0\,\,\,\left( 1 \right)\\3{x^2} + 2x + m + 2 \ge 0\,\,\,\,\,\,\,\,\;\left( 2 \right)\end{array} \right.$

- Ta có $\left( 1 \right)$ có tập nghiệm là $\mathbb{R}$ khi $\Delta ' < 0 \Leftrightarrow  - 13 + 13m < 0$$\Leftrightarrow m < 1$ (3)

- $\left( 2 \right)$ có tập nghiệm là $\mathbb{R}$ khi $\Delta ' \le 0 \Leftrightarrow  - 5 - 3m \le 0$$\Leftrightarrow m \ge  - \dfrac{5}{3}$ (4)

Từ (2) và (4), ta có $- \dfrac{5}{3} \le m < 1$.

- Ta có $f\left( x \right) = \dfrac{{2 - x}}{{x + 1}} + 2 = \dfrac{{2 - x + 2\left( {x + 1} \right)}}{{x + 1}} = \dfrac{{x + 4}}{{x + 1}}.$

Phương trình $x + 4 = 0 \Leftrightarrow x =  - \,4$ và $x + 1 = 0 \Leftrightarrow x =  - \,1.$

- Bảng xét dấu

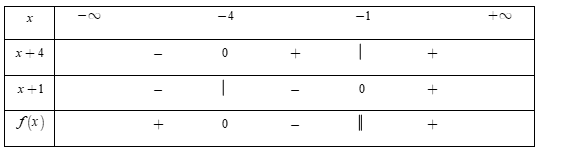
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \,4; - \,1} \right).$

Trường hợp 1:$\left\{ \begin{array}{l}\left| {x - 1} \right| - 3 > 0\\\left| {x + 2} \right| - 5 < 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x - 1 > 3\\x - 1 <  - 3\end{array} \right.\\ - 5 < x + 2 < 5\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}x > 4\\x <  - 2\end{array} \right.\\ - 7 < x < 3\end{array} \right.$$\Leftrightarrow  - 7 < x <  - 2$

Trường hợp 2: $\left\{ \begin{array}{l}\left| {x - 1} \right| - 3 < 0\\\left| {x + 2} \right| - 5 > 0\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l} - 3 < x - 1 < 3\\\left[ \begin{array}{l}x + 2 > 5\\x + 2 <  - 5\end{array} \right.\end{array} \right.$$\Leftrightarrow \left\{ \begin{array}{l} - 2 < x < 4\\\left[ \begin{array}{l}x > 3\\x <  - 7\end{array} \right.\end{array} \right.$$\Leftrightarrow 3 < x < 4$

Ta có$\sqrt { - {x^2} + 6x - 5}  > 8 - 2x$

$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{ - {x^2} + 6x - 5 \ge 0}\\{8 - 2x < 0}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{8 - 2x \ge 0}\\{ - {x^2} + 6x - 5 > {{\left( {8 - 2x} \right)}^2}}\end{array}} \right.}\end{array}} \right.$$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{1 \le x \le 5}\\{x > 4}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x \le 4}\\{ - 5{x^2} + 38x - 69 > 0}\end{array}} \right.}\end{array}} \right.$$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\left\{ {\begin{array}{*{20}{c}}{1 \le x \le 5}\\{x > 4}\end{array}} \right.}\\{\left\{ {\begin{array}{*{20}{c}}{x \le 4}\\{3 < x < \dfrac{{23}}{5}}\end{array}} \right.}\end{array}} \right.$

$\Leftrightarrow \left[ \begin{array}{l} 4 < x \le 5\\ 3 < x \le 4 \end{array} \right. \Leftrightarrow 3 < x \le 5$

Điều kiện: ${x^2} - 3x - 10 \ne 0 \Leftrightarrow \left( {x + 2} \right)\left( {x - 5} \right) \ne 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne  - \,2\\x \ne 5\end{array} \right..$

Bất phương trình $\dfrac{{ - \,2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} \le  - 1$$\Leftrightarrow \dfrac{{ - 2{x^2} + 7x + 7}}{{{x^2} - 3x - 10}} + 1 \le 0$ $\Leftrightarrow \dfrac{{ - {x^2} + 4x - 3}}{{{x^2} - 3x - 10}} \le 0\,\,\,\,\left(  *  \right)$

Bảng xét dấu

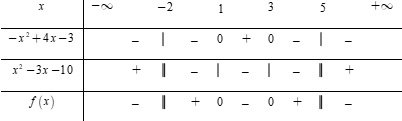
Dựa vào bảng xét dấu, bất phương trình $\left(  *  \right) \Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left[ {1;3} \right] \cup \left( {5; + \,\infty } \right).$

Bất phương trình $\left( {3x - 6} \right)\left( {x - 2} \right)\left( {x + 2} \right)\left( {x - 1} \right) > 0 \Leftrightarrow 3{\left( {x - 2} \right)^2}\left( {x + 2} \right)\left( {x - 1} \right) > 0$

Vì ${\left( {x - 2} \right)^2} > 0,\,\,\forall x \ne 2$ nên bất phương trình trở thành $\left\{ \begin{array}{l}x \ne 2\\\left( {x + 2} \right)\left( {x - 1} \right) > 0\end{array} \right..$

Đặt $f\left( x \right) = \left( {x + 2} \right)\left( {x - 1} \right).$

Phương trình $x + 2 = 0 \Leftrightarrow x =  - \,2$ và $x - 1 = 0 \Leftrightarrow x = 1.$

Ta có bảng xét dấu

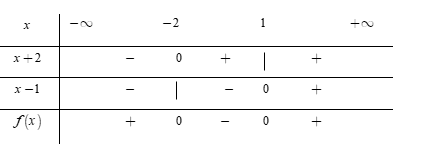
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) > 0$$\Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left( {1; + \,\infty } \right).$

Kết hợp với điều kiện $x \ne 2,$ ta được $\Leftrightarrow x \in \left( { - \,\infty ; - \,2} \right) \cup \left( {1;2} \right) \cup \left( {2; + \,\infty } \right).$

Do đó, nghiệm nguyên âm lớn nhất của bất phương trình là $- \,3$ và nghiệm nguyên dương nhỏ nhất của bất phương trình là $3.$

Vậy tích cần tính là $\left( { - \,3} \right).3 =  - \,9.$

Cách giải:

Ta có $2{x^2} - x - 6 \le 0 \Leftrightarrow  - \dfrac{3}{2} \le x \le 2,{\rm{ }}\left( I \right)$.

${x^3} + {x^2} - x - 1 \ge 0$$\Leftrightarrow \left( {x + 1} \right)\left( {{x^2} - 1} \right) \ge 0$$\Leftrightarrow \left( {x - 1} \right){\left( {x + 1} \right)^2} \ge 0$$\Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - 1}\\{x \ge 1}\end{array}} \right..{\rm{ }}\left( {II} \right)$

Từ $\left( I \right)$ và $\left( {II} \right)$ suy ra nghiệm của hệ là $S = \left[ {1;{\rm{ }}2} \right] \cup \left\{ { - 1} \right\}$.

Đặt $f\left( x \right) = 2x\left( {4 - x} \right)\left( {3 - x} \right)\left( {3 + x} \right).$

Phương trình $2x = 0 \Leftrightarrow x = 0;\,\,$$4 - x = 0 \Leftrightarrow x = 4;\,\,$

Và $3 - x = 0 \Leftrightarrow x = 3;3 + x = 0 \Leftrightarrow x =  - 3$.

Ta có bảng xét dấu:

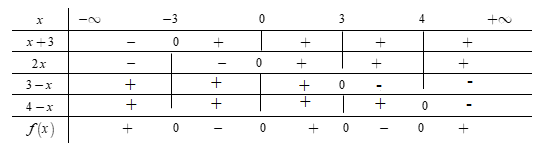
Từ bảng xét dấu ta có $f\left( x \right) > 0 \Leftrightarrow \left[ \begin{array}{l}x > 4\\0 < x < 3\\x <  - \,3\end{array} \right. \Leftrightarrow x \in \left( { - \infty ;\, - 3} \right) \cup \left( {0;\,3} \right) \cup \left( {4;\, + \infty } \right).$

Suy ra tập nghiệm bất phương trình là hợp của ba khoảng.

Điều kiện: $x\left( {x + 2} \right) \ge 0$

Đặt $f\left( x \right) = x\left( {x + 2} \right).$

Phương trình $x = 0$ và $x + 2 = 0 \Leftrightarrow x =  - \,2.$

Bảng xét dấu:

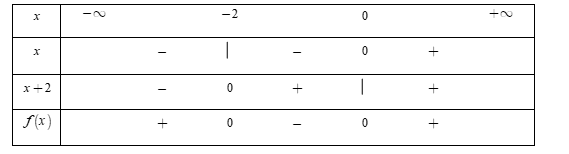
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l}x \ge 0\\x \le  - \,2\end{array} \right..$

- Nếu $f\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 2\end{array} \right.$ thì bất phương trình trở thành $0 \ge 0$ (đúng).

- Nếu $\left[ \begin{array}{l}x > 0\\x <  - 2\end{array} \right.$ thì $f\left( x \right) > 0$ nên bất phương trình tương đương $x - 1 \ge 0 \Leftrightarrow x \ge 1$.

Kết hợp $\left[ \begin{array}{l}x > 0\\x <  - 2\end{array} \right.$ ta được $x \ge 1$.

Vậy bất phương trình có tập nghiệm $S = \left\{ { - 2} \right\} \cup \left\{ 0 \right\} \cup \left[ {1; + \infty } \right)$.

Do đó nghiệm nguyên nhỏ nhất của bất phương trình là $x =  - 2$.