Bất phương trình $\dfrac{3}{{2 - x}} < 1$ có tập nghiệm là
Bất phương trình $\dfrac{3}{{2 - x}} < 1 \Leftrightarrow \dfrac{3}{{2 - x}} - 1 < 0 \Leftrightarrow \dfrac{{x + 1}}{{2 - x}} < 0.$
Đặt $f\left( x \right) = \dfrac{{x + 1}}{{2 - x}}.$ Ta có $x + 1 = 0 \Leftrightarrow x = - \,1$ và $2 - x = 0 \Leftrightarrow x = 2.$
Bảng xét dấu
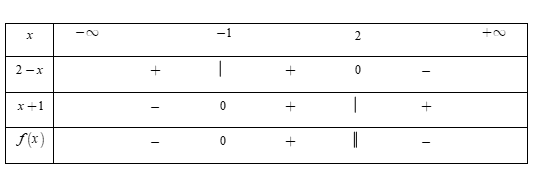
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x < - \,1\\x > 2\end{array} \right..$
Vậy tập nghiệm của bất phương trình là $S = \left( { - \,\infty ; - \,1} \right) \cup \left( {2; + \,\infty } \right).$
Số nghiệm của phương trình: $\sqrt {x + 8 - 2\sqrt {x + 7} } = 2 - \sqrt {x + 1 - \sqrt {x + 7} } $ là:
Điều kiện \(x \ge - 7\).
Đặt \(t = \sqrt {x + 7} \) , điều kiện \(t \ge 0\).
Ta có \(\sqrt {{t^2} + 1 - 2t} = 2 - \sqrt {{t^2} - 6 - t} \)\( \Leftrightarrow \left| {t - 1} \right| = 2 - \sqrt {{t^2} - t - 6} \)
Nếu \(t \ge 1\) thì ta có \(3 - t = \sqrt {{t^2} - t - 6} \)\( \Leftrightarrow \left\{ \begin{array}{l}{t^2} - t - 6 = 9 - 6t + {t^2}\\t \le 3\end{array} \right.\)\( \Leftrightarrow t = 3\)\( \Leftrightarrow \sqrt {x + 7} = 3\)\( \Leftrightarrow x = 2\)
Nếu \(t < 1\) thì ta có \(1 + t = \sqrt {{t^2} - t - 6} \)\( \Leftrightarrow \left\{ \begin{array}{l}{t^2} - t - 6 = 1 + 2t + {t^2}\\t \ge - 1\end{array} \right.\)\( \Leftrightarrow t = - \dfrac{7}{3}\;\;\left( l \right)\).
Tập nghiệm của bất phương trình $\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1$ là
Bất phương trình $\dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} \ge 1 \Leftrightarrow \dfrac{{{x^2} + x - 3}}{{{x^2} - 4}} - 1 \ge 0 \Leftrightarrow \dfrac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 2} \right)}} \ge 0.$
Đặt $f\left( x \right) = \dfrac{{x + 1}}{{\left( {x - 2} \right)\left( {x + 2} \right)}}.$ Ta có $x + 1 = 0 \Leftrightarrow x = - \,1$ và $\left( {x - 2} \right)\left( {x + 2} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = - \,2\\x = 2\end{array} \right..$
Bảng xét dấu
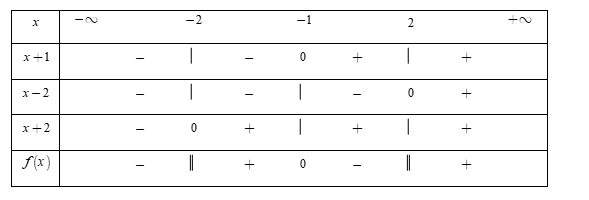
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) \ge 0 \Leftrightarrow \left[ \begin{array}{l} - \,2 < x \le - \,1\\x > 2\end{array} \right..$
Vậy tập nghiệm của bất phương trình là $S = \left( { - \,2; - \,1} \right] \cup \left( {2; + \,\infty } \right).$
Bất phương trình \(\dfrac{4}{{x - 1}} - \dfrac{2}{{x + 1}} < 0\) có tập nghiệm là
Bất phương trình \(\dfrac{4}{{x - 1}} - \dfrac{2}{{x + 1}} < 0 \Leftrightarrow \dfrac{{2x + 6}}{{\left( {x - 1} \right)\left( {x + 1} \right)}} < 0.\)
Đặt $f\left( x \right) = \dfrac{{2x + 6}}{{\left( {x - 1} \right)\left( {x + 1} \right)}}.$
Ta có $2x + 6 = 0 \Leftrightarrow x = - \,3$ và $\left( {x - 1} \right)\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - \,1\end{array} \right..$
Bảng xét dấu
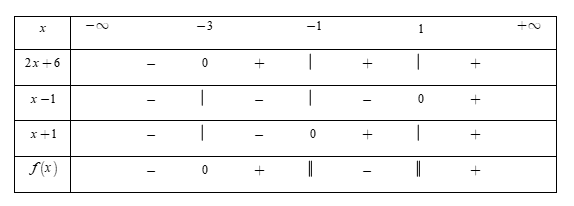
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x < - \,3\\ - \,1 < x < 1\end{array} \right..$
Vậy tập nghiệm của bất phương trình là $S = \left( { - \,\infty ; - \,3} \right) \cup \left( { - \,1;1} \right).$
Hệ bất phương trình $\left\{ \begin{array}{l}{x^2} - 1 \le 0\\x - m > 0\end{array} \right.$ có nghiệm khi
Ta có: $\left\{ \begin{array}{l}{x^2} - 1 \le 0\\x - m > 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l} - 1 \le x \le 1\\x > m\end{array} \right.$.
Do đó hệ có nghiệm khi \(m < 1\).
Bất phương trình $\dfrac{1}{{x + 1}} < \dfrac{1}{{{{\left( {x - 1} \right)}^2}}}$ có tập nghiệm \(S\) là
Bất phương trình $\dfrac{1}{{x + 1}} < \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} \Leftrightarrow \dfrac{1}{{x + 1}} - \dfrac{1}{{{{\left( {x - 1} \right)}^2}}} < 0.$
$ \Leftrightarrow \dfrac{{{{\left( {x - 1} \right)}^2} - \left( {x + 1} \right)}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}} < 0 \Leftrightarrow \dfrac{{x\left( {x - 3} \right)}}{{\left( {x + 1} \right){{\left( {x - 1} \right)}^2}}} < 0 \Leftrightarrow \left\{ \begin{array}{l}x \ne 1\\\dfrac{{x\left( {x - 3} \right)}}{{x + 1}} < 0\end{array} \right.$ (vì ${\left( {x - 1} \right)^2} > 0,\,\,\forall x \ne 1$).
Đặt $f\left( x \right) = \dfrac{{x\left( {x - 3} \right)}}{{x + 1}}.$ Ta có $x - 3 = 0 \Leftrightarrow x = 3$ và $x + 1 = 0 \Leftrightarrow x = - \,1.$
Bảng xét dấu

Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow \left[ \begin{array}{l}x < - \,1\\0 < x < 3\end{array} \right..$
Kết hợp với điều kiện $x \ne 1,$ ta được tập nghiệm $S = \left( { - \,\infty ; - \,1} \right) \cup \left( {0;1} \right) \cup \left( {1;3} \right).$
Xác định $m$ để phương trình $\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0$ có ba nghiệm phân biệt lớn hơn $–1.$
Ta có $\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0$$ \Leftrightarrow \left[ \begin{array}{l}x = 1\\{x^2} + 2\left( {m + 3} \right)x + 4m + 12 = 0\;\,\left( * \right)\end{array} \right.$.
Giả sử phương trình $\left( * \right)$ có hai nghiệm phân biệt ${x_1},{x_2}$, theo Vi-et ta có
$\left\{ \begin{array}{l}{x_1} + {x_2} = - 2\left( {m + 3} \right)\\{x_1}.{x_2} = 4m + 12\end{array} \right.$.
Để phương trình $\left( {x - 1} \right)\left[ {{x^2} + 2\left( {m + 3} \right)x + 4m + 12} \right] = 0$có ba nghiệm phân biệt lớn hơn $-1$. thì phương trình $\left( * \right)$ có hai nghiệm phân biệt ${x_1},{x_2}$ khác $1$ và đều lớn hơn $ - 1$.
$ \Leftrightarrow \left\{ \begin{array}{l}\Delta ' > 0\\1 + 2\left( {m + 3} \right) + 4m + 12 \ne 0\\{x_2} > {x_1} > - 1\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}{\left( {m + 3} \right)^2} - \left( {4m + 12} \right) > 0\\6m + 19 \ne 0\\\left( {{x_1} + 1} \right) + \left( {{x_2} + 1} \right) > 0\\\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right) > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}{m^2} + 2m - 3 > 0\\m \ne - \dfrac{{19}}{6}\\ - 2\left( {m + 3} \right) + 2 > 0\\4m + 12 - 2\left( {m + 3} \right) + 1 > 0\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m > 1\\m < - 3\end{array} \right.\\m \ne - \dfrac{{19}}{6}\\m < - 2\\m > - \dfrac{7}{2}\end{array} \right.$$ \Leftrightarrow \left\{ \begin{array}{l} - \dfrac{7}{2} < m < - 3\\m \ne - \dfrac{{19}}{6}\end{array} \right.$.
Bất phương trình $\dfrac{{x + 4}}{{{x^2} - 9}} - \dfrac{2}{{x + 3}} < \dfrac{{4x}}{{3x - {x^2}}}$ có nghiệm nguyên lớn nhất là
Bất phương trình tương đương với
$\dfrac{{x\left( {x + 4} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} - \dfrac{{2x\left( {x - 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} < - \dfrac{{4x\left( {x + 3} \right)}}{{x\left( {x - 3} \right)\left( {x + 3} \right)}} \Leftrightarrow \dfrac{{3x + 22}}{{\left( {x - 3} \right)\left( {x + 3} \right)}} < 0.$
Đặt $f\left( x \right) = \dfrac{{3x + 22}}{{\left( {x - 3} \right)\left( {x + 3} \right)}}.$
Ta có $3x + 22 = 0 \Leftrightarrow x = - \dfrac{{22}}{3};\,\,\left\{ \begin{array}{l}x - 3 = 0 \Leftrightarrow x = 3\\x + 3 = 0 \Leftrightarrow x = - \,3\end{array} \right..$
Bảng xét dấu
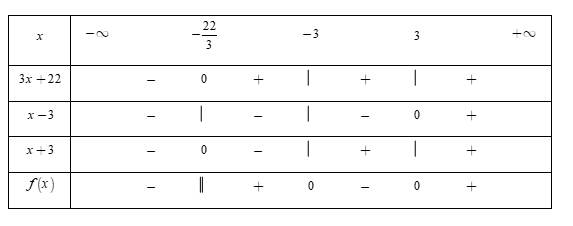
Dựa vào bảng xét dấu, ta thấy rằng $f\left( x \right) < 0 \Leftrightarrow x \in \left( { - \,\infty ; - \dfrac{{22}}{3}} \right) \cup \left( { - \,3;3} \right).$
Vậy nghiệm nguyên lớn nhất thỏa mãn bất phương trình là $x = 2.$
Để phương trình sau có 4 nghiệm phân biệt: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\) thì giá trị của tham số \(a\) là:
Xét phương trình: \(\left| {10x - 2{x^2} - 8} \right| = {x^2} - 5x + a\) (1)
\( \Leftrightarrow a = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
Xét \(f\left( x \right) = \left| {10x - 2{x^2} - 8} \right| - {x^2} + 5x\)
\( = \left\{ \begin{array}{l}\left( {10x - 2{x^2} - 8} \right) - {x^2} + 5x{\rm{ }} & {\rm{khi }}10x - 2{x^2} - 8 \ge 0\\ - \left( {10x - 2{x^2} - 8} \right) - {x^2} + 5x{\rm{ }} & {\rm{khi }}10x - 2{x^2} - 8 < 0\end{array} \right.\)
\( = \left\{ \begin{array}{l} - 3{x^2} + 15x - 8 & {\rm{khi }}1 \le x \le 4\\{x^2} - 5x + 8 & {\rm{khi }}x \le 1 \vee x \ge 4\end{array} \right.\)
Bảng biến thiên:
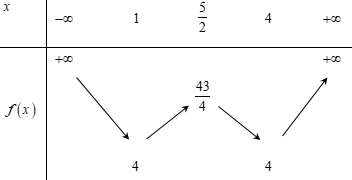
Dựa vào bảng biến thiên ta có phương trình (1) có 4 nghiệm phân biệt \( \Leftrightarrow 4 < a < \dfrac{{43}}{4}\).
Nghiệm của bất phương trình $\left| {2x - 3} \right| \le 1$ là
Ta có $\left| {2x - 3} \right| \le 1 \Leftrightarrow - \,1 \le 2x - 3 \le 1 \Leftrightarrow 2 \le 2x \le 4 \Leftrightarrow 1 \le x \le 2.$
Để bất phương trình \(\sqrt {(x + 5)(3 - x)} \le {x^2} + 2x + a\) nghiệm đúng \(\forall x \in \left[ { - 5;3} \right]\), tham số \(a\) phải thỏa điều kiện:
\(\sqrt {\left( {x + 5} \right)\left( {3 - x} \right)} \le {x^2} + 2x + a \Leftrightarrow \sqrt { - {x^2} - 2x + 15} - {x^2} - 2x \le a\)
Đặt \(t = \sqrt { - {x^2} - 2x + 15} \), ta có bảng biến thiên
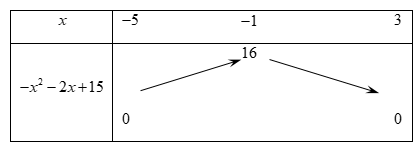
Suy ra \(t \in \left[ {0;4} \right]\).
Bất phương trình đã cho thành ${t^2} + t - 15 \le a$.
Xét hàm $f\left( t \right) = {t^2} + t - 15$ với \(t \in \left[ {0;4} \right]\)
Ta có bảng biến thiên
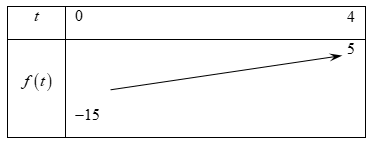
Bất phương trình \({t^2} + t - 15 \le a\) nghiệm đúng \(\forall t \in \left[ {0;4} \right]\) khi và chỉ khi \(a \ge 5.\)
Tập nghiệm của bất phương trình $\left| {x - 3} \right| > - 1$ là
Vì $\left| {x - 3} \right| \ge 0,\,\,\forall x \in \mathbb{R}$ nên suy ra $\left| {x - 3} \right| > - 1,\,\,\forall x \in \mathbb{R}.$
Vậy tập nghiệm của bất phương trình là $S = \mathbb{R}.$
Cho bất phương trình: ${x^2} - 2x \le \left| {x - 2} \right| + ax - 6$. Giá trị dương nhỏ nhất của $a$ để bất phương trình có nghiệm gần nhất với số nào sau đây:
Trường hợp 1: $x \in \left[ {2; + \infty } \right)$.
Khi đó bất phương trình đã cho trở thành:
${x^2} - \left( {a + 3} \right)x + 8 \le 0$$ \Leftrightarrow a \ge x + \dfrac{8}{x} - 3 \ge 4\sqrt 2 - 3 \approx 2,65$$\forall x \in \left[ {2; + \infty } \right)$.
Dấu xảy ra khi $x = 2\sqrt 2 $.
Trường hợp 2: $x \in \left( { - \infty ;2} \right)$.
Khi đó bất phương trình đã cho trở thành:
${x^2} - \left( {a + 1} \right)x + 4 \le 0$
$\Leftrightarrow ax \ge {x^2} -x+4$
$ \Leftrightarrow \left[ \begin{array}{l}a \ge \dfrac{{x^2} -x+4}{x}\;\;khi\;\;x \in \left( {0;2} \right)\;\;\;\;\;\;\\a \le \dfrac{{x^2} -x+4}{x}\;\;khi\;\;x \in \left( { - \infty ;0} \right)\;\;\;\end{array} \right.$.
$ \Leftrightarrow \left[ \begin{array}{l}a \ge x + \dfrac{4}{x} - 1\;\;khi\;\;x \in \left( {0;2} \right)\;\;\;\;\;\;\left( 1 \right)\\a \le x + \dfrac{4}{x} - 1\;\;khi\;\;x \in \left( { - \infty ;0} \right)\;\;\;\left( 2 \right)\end{array} \right.$.
Giải $\left( 1 \right)$ ta được $a > 3$ (theo bất đẳng thức Cauchy).
Giải $\left( 2 \right)$: $a \le x + \dfrac{4}{x} - 1$$ \Leftrightarrow a \le - 2\sqrt {x.\dfrac{4}{x}} - 1 = - 5$.
Vậy giá trị dương nhỏ nhất của $a$ gần với số $2,6$.
Tập nghiệm của bất phương trình $\left| {5x - 4} \right| \ge 6$ có dạng $S = \left( { - \,\infty ;a} \right] \cup \left[ {b; + \,\infty } \right).$ Tính tổng $P = 5a + b.$
Bất phương trình $\left| {5x - 4} \right| \ge 6 \Leftrightarrow \left[ \begin{array}{l}5x - 4 \ge 6\\5x - 4 \le - \,6\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}5x \ge 10\\5x \le - \,2\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}x \ge 2\\x \le - \dfrac{2}{5}\end{array} \right..$
Do đó, tập nghiệm của bất phương trình là $S = \left( { - \,\infty ; - \dfrac{2}{5}} \right] \cup \left[ {2; + \,\infty } \right).$
Mà $S = \left( { - \,\infty ;a} \right] \cup \left[ {b; + \,\infty } \right)$ nên $\left\{ \begin{array}{l}a = - \dfrac{2}{5}\\b = 2\end{array} \right.$
Vậy \(P = 5a + b = 5.\left( { - \dfrac{2}{5}} \right) + 2 = 0\)
Bất phương trình: $\left| {{x^4} - 2{x^2} - 3} \right| \le {x^2} - 5$ có bao nhiêu nghiệm nghiệm nguyên?
Đặt \(t = {x^2} \ge 0\)
Ta có \(\left| {{t^2} - 2t - 3} \right| \le t - 5\).
Nếu \({t^2} - 2t - 3 \ge 0 \Leftrightarrow \left[ \begin{array}{l}t \le - 1\\t \ge 3\end{array} \right.\) thì ta có \({t^2} - 3t + 2 \le 0 \Leftrightarrow 1 \le t \le 2\) loại
Nếu \({t^2} - 2t - 3 < 0 \Leftrightarrow - 1 < t < 3\) thì ta có \( - {t^2} + t + 8 \le 0 \Leftrightarrow \left[ \begin{array}{l}t \le \dfrac{{1 - \sqrt {33} }}{2}\\t \ge \dfrac{{1 + \sqrt {33} }}{2}\end{array} \right.\) loại.
Bất phương trình : $\left| {3x - 3} \right| \le \left| {2x + 1} \right|$ có nghiệm là
Ta có $\left| {3x - 3} \right| \le \left| {2x + 1} \right| \Leftrightarrow {\left| {3x - 3} \right|^2} \le {\left| {2x + 1} \right|^2} \Leftrightarrow {\left( {3x - 3} \right)^2} - {\left( {2x + 1} \right)^2} \le 0$
$ \Leftrightarrow \left( {3x - 3 - 2x - 1} \right)\left( {3x - 3 + 2x + 1} \right) \le 0 \Leftrightarrow \left( {x - 4} \right)\left( {5x - 2} \right) \le 0 $
Xét dấu \(\left( {x - 4} \right)\left( {5x - 2} \right)\) ta được:
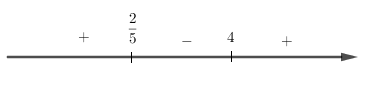
Suy ra $\dfrac{2}{5} \le x \le 4$
Vậy tập nghiệm của bất phương trình là $S = \left[ {\dfrac{2}{5};4} \right].$
Để phương trình: $\left| {x + 3} \right|(x - 2) + m - 1 = 0$có đúng một nghiệm, các giá trị của tham số \(m\)là:
Ta có $\left| {x + 3} \right|\left( {x - 2} \right) + m - 1 = 0 \Leftrightarrow m = 1 - \left| {x + 3} \right|\left( {x - 2} \right)$
Xét hàm số $y = 1 - \left| {x + 3} \right|(x - 2)$
Ta có $y = \left\{ \begin{array}{l} - {x^2} - x + 7\,\,\;khi\,\,\;x \ge - 3\\{x^2} + x - 5\,\,\;\;\;khi\,\;\;x < - 3\end{array} \right.$
Bảng biến thiên của $y = 1 - \left| {x + 3} \right|(x - 2)$
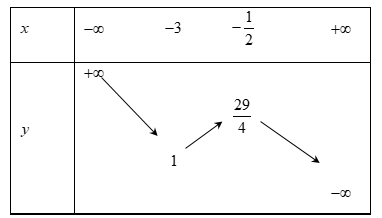
Dựa vào bảng trên phương trình có đúng $1$ nghiệm khi và chỉ khi$\left[ \begin{array}{l}m < 1\\m > \dfrac{{29}}{4}\end{array} \right.$
Hỏi có bao nhiêu giá trị nguyên $x$ trong $\left[ { - \,2017;2017} \right]$ thỏa mãn bất phương trình \(\left| {2x + 1} \right| < 3x\) ?
TH1. Với $2x + 1 \ge 0 \Leftrightarrow x \ge - \dfrac{1}{2},$ khi đó $\left| {2x + 1} \right| < 3x \Leftrightarrow 2x + 1 < 3x \Leftrightarrow x > 1.$
Kết hợp với điều kiện $x \ge - \dfrac{1}{2}$ suy ra ${S_1} = \left( {1; + \,\infty } \right).$
TH2. Với $2x + 1 < 0 \Leftrightarrow x < - \dfrac{1}{2},$ khi đó $\left| {2x + 1} \right| < 3x \Leftrightarrow - \,2x - 1 < 3x $ $\Leftrightarrow x > - \dfrac{1}{5}.$
Kết hợp với điều kiện $x < - \dfrac{1}{2}$ suy ra ${S_2} = \emptyset .$
Suy ra tập nghiệm của bất phương trình là $S = {S_1} \cup {S_2} = \left( {1; + \,\infty } \right).$
Mà \(x \in \left[ { - 2017;2017} \right]\) nên \(x \in \left( {1;2017} \right]\) hay \(x \in \left\{ {2;3;...;2017} \right\}\)
Vậy có \(2016\) giá trị nguyên của \(x\) thỏa mãn.
Bất phương trình \(\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \) có nghiệm là
TXĐ: \(D = \mathbb{R}\)
\(\left( {x + 1} \right)\left( {x + 4} \right) < 5\sqrt {{x^2} + 5x + 28} \)\( \Leftrightarrow {x^2} + 5x + 4 - 5\sqrt {{x^2} + 5x + 28} < 0\)(1)
Đặt \(\sqrt {{x^2} + 5x + 28} = t\left( {t > 0} \right)\)
(1) trở thành: \({t^2} - 5t - 24 < 0 \Leftrightarrow - 3 < t < 8\)
\(\begin{array}{l} \Rightarrow {x^2} + 5x + 28 < 64\\ \Leftrightarrow {x^2} + 5x - 36 < 0 \Leftrightarrow - 9 < x < 4\end{array}\)
Số nghiệm nguyên thỏa mãn bất phương trình $\left| {x + 2} \right| + \left| { - 2x + 1} \right| \le x + 1$ là
Xét bất phương trình $\left| {x + 2} \right| + \left| { - \,2x + 1} \right| \le x + 1\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left( * \right).$
Bảng xét dấu
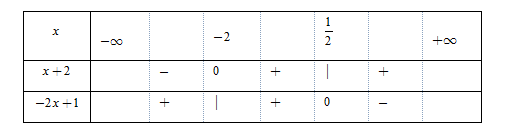
TH1. Với $x < - \,2,$ khi đó $\left( * \right) \Leftrightarrow \left( { - \,x - 2} \right) + \left( { - \,2x + 1} \right) \le x + 1 $$\Leftrightarrow - \,2 \le 4x \Leftrightarrow x \ge - \dfrac{1}{2}.$
Kết hợp với điều kiện $x < - \,2,$ ta được tập nghiệm ${S_1} = \emptyset .$
TH2. Với $ - \,2 \le x < \dfrac{1}{2},$ khi đó $\left( * \right) \Leftrightarrow x + 2 - 2x + 1 \le x + 1 $$\Leftrightarrow 2x \ge 2 \Leftrightarrow x \ge 1.$
Kết hợp với điều kiện $ - \,2 \le x < \dfrac{1}{2},$ ta được tập nghiệm ${S_2} = \emptyset .$
TH3. Với $x \ge \dfrac{1}{2},$ khi đó $\left( * \right) \Leftrightarrow x + 2 - \left( { - 2x + 1} \right) \le x + 1 $$\Leftrightarrow 2x \le 0 \Leftrightarrow x \le 0.$
Kết hợp với điều kiện $x \ge \dfrac{1}{2},$ ta được tập nghiệm ${S_3} = \emptyset .$
Vậy tập nghiệm của bất phương trình là $S = {S_1} \cup {S_2} \cup {S_3} = \emptyset .$

