Câu hỏi:
3 năm trước
Giải bất phương trình $x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right)$ ta được nghiệm:
Trả lời bởi giáo viên
Đáp án đúng: c
Bất phương trình $x\left( {x + 5} \right) \le 2\left( {{x^2} + 2} \right) \Leftrightarrow {x^2} + 5x \le 2{x^2} + 4 \Leftrightarrow {x^2} - 5x + 4 \ge 0$
Xét phương trình ${x^2} - 5x + 4 = 0 \Leftrightarrow \left( {x - 1} \right)\left( {x - 4} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = 4\end{array} \right..$
Lập bảng xét dấu:
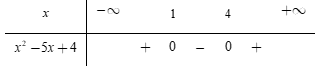
Dựa vào bảng xét dấu, ta thấy nghiệm của bất phương trình ${x^2} - 5x + 4 \ge 0$ là $ x \in \left( { - \,\infty ;1} \right] \cup \left[ {4; + \,\infty } \right).$
Hướng dẫn giải:
- Biến đổi bất phương trình đã cho về dạng bất phương trình bậc hai.
- Xét dấu vế trái và kết luận tập nghiệm.

