Cho tam giác nhọn \(ABC\). Gọi \(O\) là trung điểm của \(BC\). Dựng đường tròn tâm \(O\) đường kính \(BC\). Vẽ đường cao \(AD\) của tam giác \(ABC\) và các tiếp tuyến \(AM,AN\) với đường tròn \(\left( O \right)\) (\(M,N\) là các tiếp điểm). Gọi \(E\) là giao điểm của \(MN\) với \(AD\). Chọn câu đúng.
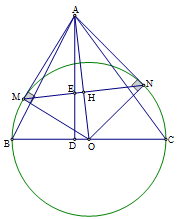
\(AM,AN\) là các tiếp tuyến của đường tròn \(\left( O \right)\), gọi \(H\) là giao điểm của \(AO\) và \(MN\).
Theo tính chất hai tiếp tuyến cắt nhau ta có \(AM = AN;\,OM = ON\) nên \(AO\) là đường trung trực của đoạn \(MN.\)
Suy ra \(AO \bot MN.\)
Ta có tam giác \(AHE\) đồng dạng với tam giác \(ADO\) (vì \(\widehat {AHE} = \widehat {ADO} = 90^\circ ;\widehat {DAO}\) chung)
nên \(AE.AD = AH.AO\). (1)
Cũng theo hệ thức lượng trong tam giác vuông \(AMO\) ta có: \(AH.AO = A{M^2}\). (2)
Từ (1) và (2) suy ra \(AE.AD = A{M^2}.\)
Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( {O;R} \right)\), \(AH\) là đường cao \(\left( {H \in BC} \right)\). Chọn câu đúng.
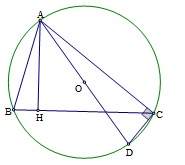
Vẽ đường kính \(AD\) của đường tròn \(\left( O \right)\), suy ra \(\widehat {ACD} = {90^0}\) (vì tam giác \(ACD\) có ba đỉnh thuộc đường tròn và \(AD\) là đường kính)
Xét \(\Delta HBA\) và \(\Delta CDA\) có:
\(\widehat {AHB} = \widehat {ACD}\left( { = {{90}^0}} \right);\widehat {HBA} = \widehat {CDA}\) (góc nội tiếp cùng chắn ),
Do đó \(\Delta HBA \backsim \Delta CDA \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{AD}} \Rightarrow AB.AC = AD.AH\). Mà \(AD = 2R\).
Do đó \(AB.AC = 2R.AH\).
Cho tam giác \(ABC\) có ba góc nhọn nội tiếp trong đường tròn \(\left( {O;R} \right)\) và hai đường cao \(AE,BF\) cắt nhau tại \(H\)(\(E \in BC,F \in AC\)).
Bốn điểm \(A,B,E,F\) cùng nằm trên một đường tròn nào sau đây?
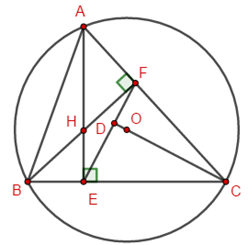
Ta có: \(AE,BF\) là đường cao của tam giác \(ABC\) nên \(AE \bot BC,\,\,BF \bot AC\).
\( \Rightarrow \angle AEB = \angle AFB = {90^0}\).
\( \Rightarrow ABEF\) nội tiếp một đường tròn đường kính AB(tứ giác có 2 đỉnh kề một cạnh cùng nhìn cạnh đối diện các góc bằng nhau)
Cho tam giác \(ABC\) có ba góc nhọn nội tiếp trong đường tròn \(\left( {O;R} \right)\) và hai đường cao \(AE,BF\) cắt nhau tại \(H\)(\(E \in BC,F \in AC\)).
Chọn câu đúng
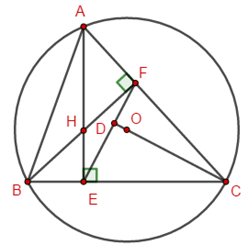
Gọi \(D\) là giao điểm của \(OC\) và \(EF\).
Ta có: \(\left\{ \begin{array}{l}\angle ACO + \angle CAO = {180^0} - \angle AOC\\\angle ACO = \angle CAO\end{array} \right.\) (do tam giác \(OAC\) cân tại \(O\)).
\( \Rightarrow \angle ACO = \angle CAO = {90^0} - \dfrac{1}{2}\angle AOC\,\,\,\left( 1 \right)\)
Mà \(\angle AOC = 2\angle ABC\) (2) (góc nội tiếp và góc ở tâm cùng chắn cung \(AC\)).
\(\angle ABC = \angle DFC\) (3) (góc ngoài và góc trong tại đỉnh đối diện của tứ giác nội tiếp \(ABEF\)).
Từ (1), (2), (3) ta được:
\(\begin{array}{l}\angle ACO = {90^0} - \angle ABC = {90^0} - \angle DFC \Rightarrow \angle ACO + \angle DFC = {90^0}\\ \Rightarrow \angle FDC = {90^0}\end{array}\)
Vậy \(OC \bot EF\).

