Câu hỏi:
3 năm trước
Cho tam giác \(ABC\) có ba góc nhọn nội tiếp trong đường tròn \(\left( {O;R} \right)\) và hai đường cao \(AE,BF\) cắt nhau tại \(H\)(\(E \in BC,F \in AC\)).
Bốn điểm \(A,B,E,F\) cùng nằm trên một đường tròn nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: b
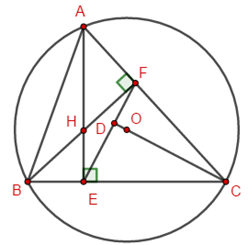
Ta có: \(AE,BF\) là đường cao của tam giác \(ABC\) nên \(AE \bot BC,\,\,BF \bot AC\).
\( \Rightarrow \angle AEB = \angle AFB = {90^0}\).
\( \Rightarrow ABEF\) nội tiếp một đường tròn đường kính AB(tứ giác có 2 đỉnh kề một cạnh cùng nhìn cạnh đối diện các góc bằng nhau)
Hướng dẫn giải:
Vận dụng dấu hiệu nhận biết của tứ giác nội tiếp: Tứ giác có 2 đỉnh kề một cạnh cùng nhìn cạnh đối diện các góc bằng nhau nên \(ABEF\) nội tiếp một đường tròn từ đó ta có điều phải chứng minh.

