Câu hỏi:
2 năm trước
Cho đường tròn $\left( {O;R} \right),$ đường kính $AB$ cố định và dây $AC.$ Biết rằng khoảng cách từ $O$ lần lượt đến $AC$ và $BC$ là $8{\rm{ }}cm$ và $6{\rm{ }}cm.$ Lấy $D$ đối xứng với $A$ qua $C.$ Chọn câu sai ?
Trả lời bởi giáo viên
Đáp án đúng: d
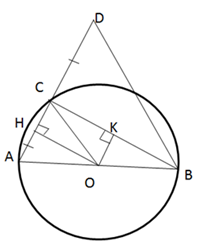
Kẻ $OH,{\rm{ }}OK$ lần lượt vuông góc với $AC$ và $BC,$ ta có :
$OH = 8\left( {cm} \right);OK = 6\left( {cm} \right)$ và \(HA = HC = \dfrac{{AC}}{2}\) ; \(KB = KC = \dfrac{{BC}}{2}\) (định lí đường kính dây cung).
$AB$ là đường kính nên \(\widehat {ACB} = {90^0}\).
Do đó tứ giác $CHOK$ là hình chữ nhật (có ba góc vuông)
$ \Rightarrow OH = CK = 8\left( {cm} \right) \Rightarrow BC = 16{\rm{ }}\left( {cm} \right)$
Tương tự có: $AC = 12\left( {cm} \right)$
Xét tam giác vuông $OHC,$ ta có: \(OC = \sqrt {O{H^2} + H{C^2}} = \sqrt {{8^2} + {6^2}} = 10\,\,\left( {cm} \right)\) (định lý Py – ta – go)
$\Delta ABD$ có đường cao $BC$ đồng thời là đường trung tuyến nên $\Delta ABD$ cân tại $B.$
Ta có $BD = BA = 2R\left( {cm} \right),$ điểm $B$ cố định, $2R$ không đổi.
Vậy $D$ thuộc đường tròn cố định tâm $B$ và bán kính bằng $2R.$ Do đó D sai.
Hướng dẫn giải:
+ Sử dụng : Đường kính vuông góc với dây thì đi qua trung điểm của dây đó.
+ Chứng minh tam giác \(ABD\) cân từ đó tính \(BD\) suy ra quỹ tích điểm \(D.\)
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
