Câu hỏi:
2 năm trước
Cho tam giác nhọn \(ABC\). Gọi \(O\) là trung điểm của \(BC\). Dựng đường tròn tâm \(O\) đường kính \(BC\). Vẽ đường cao \(AD\) của tam giác \(ABC\) và các tiếp tuyến \(AM,AN\) với đường tròn \(\left( O \right)\) (\(M,N\) là các tiếp điểm). Gọi \(E\) là giao điểm của \(MN\) với \(AD\). Chọn câu đúng.
Trả lời bởi giáo viên
Đáp án đúng: b
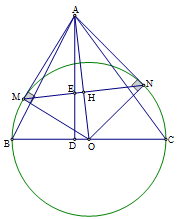
\(AM,AN\) là các tiếp tuyến của đường tròn \(\left( O \right)\), gọi \(H\) là giao điểm của \(AO\) và \(MN\).
Theo tính chất hai tiếp tuyến cắt nhau ta có \(AM = AN;\,OM = ON\) nên \(AO\) là đường trung trực của đoạn \(MN.\)
Suy ra \(AO \bot MN.\)
Ta có tam giác \(AHE\) đồng dạng với tam giác \(ADO\) (vì \(\widehat {AHE} = \widehat {ADO} = 90^\circ ;\widehat {DAO}\) chung)
nên \(AE.AD = AH.AO\). (1)
Cũng theo hệ thức lượng trong tam giác vuông \(AMO\) ta có: \(AH.AO = A{M^2}\). (2)
Từ (1) và (2) suy ra \(AE.AD = A{M^2}.\)
Hướng dẫn giải:
+ Sử dụng tính chất hai tiếp tuyến cắt nhau để chỉ ra \(AO \bot MN.\)
+ Gọi \(H\) là giao điểm của \(AO\) và \(MN\).
+ Sử dụng tính chất hai tam giác đồng dạng và hệ thức lượng trong tam giác vuông để tìm hệ thức đúng.
Câu hỏi khác
- Bài tập tính chất hai tiếp tuyến cắt nhau toán 9 có lời giải
- Bài tập sự xác định của đường tròn- tính chất đối xứng của đường tròn toán 9 có lời giải
- Bài tập vị trí tương đối giữa đường thẳng và đường tròn toán 9 có lời giải
- Bài tập đường kính và dây của đường tròn toán 9 có lời giải
- Bài tập dấu hiệu nhận biết tiếp tuyến của đường tròn toán 9 có lời giải
