Cho tam giác \(ABC\) nội tiếp đường tròn \(\left( {O;R} \right)\), \(AH\) là đường cao \(\left( {H \in BC} \right)\). Chọn câu đúng.
Trả lời bởi giáo viên
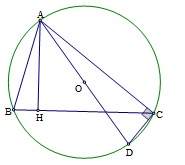
Vẽ đường kính \(AD\) của đường tròn \(\left( O \right)\), suy ra \(\widehat {ACD} = {90^0}\) (vì tam giác \(ACD\) có ba đỉnh thuộc đường tròn và \(AD\) là đường kính)
Xét \(\Delta HBA\) và \(\Delta CDA\) có:
\(\widehat {AHB} = \widehat {ACD}\left( { = {{90}^0}} \right);\widehat {HBA} = \widehat {CDA}\) (góc nội tiếp cùng chắn ),
Do đó \(\Delta HBA \backsim \Delta CDA \Rightarrow \dfrac{{AH}}{{AC}} = \dfrac{{AB}}{{AD}} \Rightarrow AB.AC = AD.AH\). Mà \(AD = 2R\).
Do đó \(AB.AC = 2R.AH\).
Hướng dẫn giải:
Vẽ đường kính \(AD\) của đường tròn \(\left( O \right)\)
Sử dụng tính chất hai tam giác đồng dạng để tìm hệ thức đúng.

