Cho hình chóp $SABC$ có $SA \bot \left( {ABC} \right).$ Gọi $H,{\rm{ }}K$ lần lượt là trực tâm các tam giác $SBC$ và$ABC$. Mệnh đề nào sai trong các mệnh đề sau?
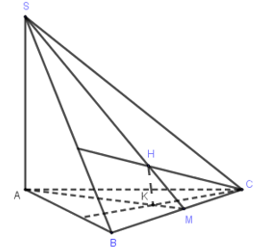
Ta có\(BC \bot SA,\,BC\, \bot SH\,\, \Rightarrow \,BC \bot (SAH)\)
Ta có \(CK \bot AB,CK \bot SA \Rightarrow CK \bot (SAB)\) hay \(CK \bot SB\)
Mặt khác có \(CH \bot SB\) nên \(SB \bot (CHK)\) hay \(SB \bot HK\).
Ta có:
\(\left\{ \begin{array}{l}
BK \bot AC\\
BK \bot SA
\end{array} \right. \) \(\Rightarrow BK \bot \left( {SAC} \right) \Rightarrow BK \bot SC\)
Mà \(BH \bot SC\) nên \(SC \bot (BHK)\) nên \(SC \bot HK\).
Do đó \(HK \bot (SBC)\).
Gọi \(M\) là giao điểm của \(SH\) và \(BC\). Do \(BC \bot (SAH)\,\, \Rightarrow BC \bot AM\) hay đường thẳng
\(AM\) trùng với đường thẳng \(AK\). Hay $SH,AK$ và $BC$ đồng quy.
Do đó $BC \bot \left( {SAB} \right)$ là sai.
Cho hai hình chữ nhật $ABCD$ và $ABEF$ nằm trong hai mặt phẳng khác nhau sao cho hai đường thẳng $AC$ và $BF$ vuông góc với nhau. Gọi $CH$ và $FK$ lần lượt là đường cao của hai tam giác $BCE$ và $ADF$.
Khẳng định nào sau đây là sai?
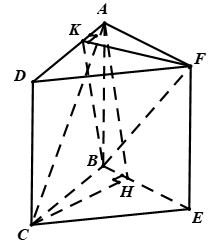
Ta có $\left. \begin{array}{l}AB \bot BC\\AB \bot BE\end{array} \right\} \Rightarrow AB \bot \left( {BCE} \right)$
Vậy $\left\{ \begin{array}{l}CH \bot AB\\CH \bot BE\end{array} \right. \Rightarrow CH \bot \left( {ABEF} \right)$
Ta có $CH \bot \left( {ABEF} \right) \Rightarrow CH \bot BF$, mặt khác $AC \bot BF \Rightarrow BF \bot \left( {ACH} \right) \Rightarrow BF \bot AH$.
Tương tự $\left. \begin{array}{l}AC \bot KF\\AC \bot BF\end{array} \right\} \Rightarrow AC \bot \left( {BKF} \right) \Rightarrow AC \bot BK$.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình vuông và \(SA \bot \left( {ABCD} \right)\). Gọi \(I\), \(J\), \(K\) lần lượt là trung điểm của \(AB\), \(BC\) và \(SB\). Khẳng định nào sau đây sai?
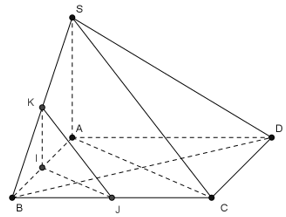
Do \(IJ\;{\rm{//}}\;AC\) và \(IK{\rm{//}}SA\) nên \(\left( {IJK} \right){\rm{//}}\left( {SAC} \right)\). Vậy A đúng.
Do \(BD \bot AC\) và \(BD \bot SA\) nên \(BD \bot \left( {SAC} \right)\) nên D đúng.
Do \(BD \bot \left( {SAC} \right)\) và \(\left( {IJK} \right){\rm{//}}\left( {SAC} \right)\) nên \(BD \bot \left( {IJK} \right)\) nên B đúng.
Vậy C sai.
Cho hình tứ diện \(ABCD\) có $AB$, $BC$, $CD$ đôi một vuông góc nhau. Hãy chỉ ra điểm \(O\) cách đều bốn điểm \(A\), \(B\), \(C\), \(D\).
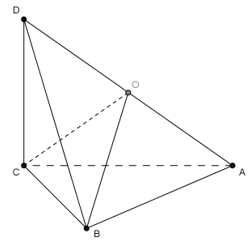
Gọi \(O\) là trung điểm của \(AD\).
Từ giả thiết ta có \(\left\{ \begin{array}{l}AB \bot CD\\BC \bot CD\end{array} \right. \Rightarrow CD \bot \left( {ABC} \right) \Rightarrow CD \bot AC\). Vậy $\Delta ACD$ vuông tại \(C\).
Do đó \(OA = OC = OD\) (1)
Mặt khác \(\left\{ \begin{array}{l}AB \bot CD\\AB \bot BC\end{array} \right. \Rightarrow AB \bot \left( {BCD} \right) \Rightarrow AB \bot BD \Rightarrow \Delta ABD\) vuông tại \(B\).
Do đó \(OA = OB = OD\) (2)
Từ (1) và (2) ta có \(OA = OB = OC = OD\).
Cho hình chóp $S.ABCD$ có đáy $ABCD$ là hình vuông cạnh $a$, mặt bên $SAB$ là tam giác đều và $SC = a\sqrt 2 $. Gọi $H,K$ lần lượt là trung điểm của các cạnh $AB$ và $AD$. Khẳng định nào sau đây là sai?.
Vì $H$ là trung điểm của $AB$ và tam giác $SAB$ đều nên $SH \bot AB$
Lại có $SH = \dfrac{{a\sqrt 3 }}{2},SC = a\sqrt 2 ,$ $HC = \sqrt {B{H^2} + B{C^2}} = \dfrac{{a\sqrt 5 }}{2}$
Do đó $H{C^2} + H{S^2} = \dfrac{{3{a^2}}}{4} + \dfrac{{5{a^2}}}{4} = 2{a^2} = S{C^2}$
$ \Rightarrow \Delta HSC$ vuông tại $H \Rightarrow SH \bot HC$ nên B đúng.
Vậy $\left\{ \begin{array}{l}SH \bot HC\\SH \bot AB\end{array} \right. \Rightarrow SH \bot \left( {ABCD} \right)$ nên A đúng.
b) Ta có $AC \bot HK$ và $AC \bot SH \Rightarrow AC \bot \left( {SHK} \right)$
$ \Rightarrow AC \bot SK$ nên C đúng.
Cho hình chóp $S.ABC$ có $\widehat {BSC} = {120^0},\widehat {CSA} = {60^0},\widehat {ASB} = {90^0},$ $SA = SB = SC.$ Gọi $I$ là hình chiếu vuông góc của $S$ lên $mp\left( {ABC} \right).$ Chọn khẳng định đúng trong các khẳng định sau
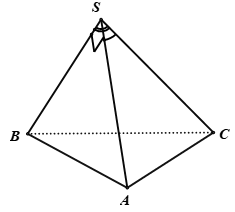
Gọi \(SA = SB = SC = a\)
Ta có :$\vartriangle SAC$ đều \( \Rightarrow AC = SA = a\)
$\vartriangle SAB$ vuông cân tại $S$ \( \Rightarrow AB = a\sqrt 2 \)
\(BC = \sqrt {S{B^2} + S{C^2} - 2SB.SC.\cos \widehat {BSC}} = a\sqrt 3 \)
$\vartriangle ABC$ vuông tại $A$
Gọi $I$ là trung điểm của $AC$ thì là tâm đường tròn
ngoại tiếp tam giác $ABC.$
Do \(SA = SB = SC\) và \(IA = IB = IC\) nên \(SI \bot \left( {ABC} \right)\).
Vậy \(I\) là hình chiếu vuông góc của $S$ lên mặt phẳng $\left( {ABC} \right)$
Cho tứ diện $OABC$ có $OA,OB,OC$ đôi một vuông góc với nhau. Gọi $H$ là hình chiếu của $O$ trên mặt phẳng $\left( {ABC} \right)$. Xét các mệnh đề sau :
I. Vì $OC \bot OA,OC \bot OB$ nên $OC \bot \left( {OAB} \right)$.
II. Do $AB \subset \left( {OAB} \right)$nên $AB \bot OC.{\rm{ }}\left( 1 \right)$
III. Có $OH \bot \left( {ABC} \right)$ và $AB \subset \left( {ABC} \right)$nên $AB \bot OH.{\rm{ }}\left( 2 \right)$
IV. Từ $\left( 1 \right)$ và $\left( 2 \right) \Rightarrow AB \bot \left( {OCH} \right)$
Số mệnh đề đúng trong các mệnh đề trên là:
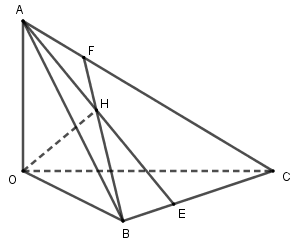Ta có:
$\left\{ \begin{array}{l}OC \bot OA\\OC \bot OB\\OA \cap OB = O\\OA,OB \subset \left( {OAB} \right)\end{array} \right. \Rightarrow OC \bot \left( {OAB} \right)$.
Vậy $I$ đúng.
$\left\{ \begin{array}{l}OC \bot \left( {OAB} \right)\\AB \subset \left( {OAB} \right)\end{array} \right. \Rightarrow AB \bot OC$.
Vậy $II$ đúng.
$\left\{ \begin{array}{l}OH \bot \left( {ABC} \right)\\AB \subset \left( {ABC} \right)\end{array} \right. \Rightarrow AB \bot OH$.
Vậy $III$ đúng.
$\left\{ {\begin{array}{*{20}{c}}{AB \bot OC}\\{AB \bot OH}\\\begin{array}{l}OC \cap OH = O\\OC,OH \subset \left( {OCH} \right)\end{array}\end{array}} \right. \Rightarrow AB \bot \left( {OCH} \right)$.
Vậy $IV$ đúng.
Cho hình hộp $ABCD.A'B'C'D'$ có đáy là hình thoi $\widehat {BAD} = {60^0}$ và $A'A = A'B = A'D$. Gọi $O = AC \cap BD$. Hình chiếu của $A'$ trên $\left( {ABCD} \right)$ là :
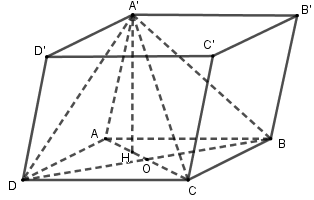
Vì $A'A = A'B = A'D \Rightarrow $ hình chiếu của \(A'\) trên $\left( {ABCD} \right)$ trùng với \(H\) là tâm đường tròn ngoại tiếp \(\Delta ABD\,\,\left( 1 \right).\)
Mà tứ giác \(ABCD\) là hình thoi và $\widehat {BAD} = {60^0}$ nên \(\Delta BAD\) là tam giác đều \(\left( 2 \right)\)
Từ \(\left( 1 \right)\,\)và \(\left( 2 \right) \Rightarrow H\) là trọng tâm \(\Delta ABD\,.\)
Cho hình chóp S.ABCD có đáy ABCD là hình vuông và \(SA \bot (ABCD)\). Mệnh đề nào đưới đây sai?
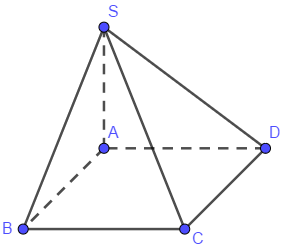
Đáp án C sai vì nếu \(AC \bot (SBD)\) thì \(AC \bot SO\left( {\left\{ O \right\} = AC \cap BD} \right)\)
Điều này không thể xảy ra vì từ S chỉ có thể kẻ được 1 đường thẳng \(SA \bot AC\).
Hình bên là một bộ đèn chùm 10 bóng.
Biết \(S.ABCD\) là một hình chóp đều. Cảc cạnh bên là ba đoạn dây treo, \(AB = 44\;{\rm{cm}}\). Các cạnh đáy là ống thép tròn đều, \(BC = 68\;{\rm{cm}}\). Bộ đèn được treo lên trần nhà bởi đoạn dây \(SA\)
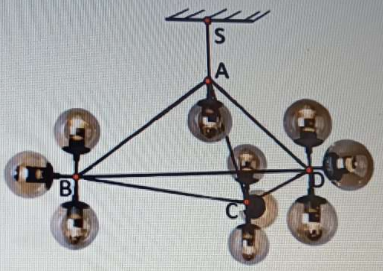
Tính góc giữa hai đường thẳng \(SA\)và \(AB\).
Kẻ \(AH \bot \left( {BCD} \right)\), khi đó S,A,H thẳng hàng.
Gọi góc giữa hai đường thẳng \(SA\) và \(AB\) là \(\alpha \).
H là trọng tâm \(\Delta BCD\)
\( \Rightarrow BH = \dfrac{{68\sqrt 3 }}{3}(cm)\)
\(\sin \alpha = \dfrac{{BH}}{{AB}} = \dfrac{{62\sqrt 3 /3}}{{44}} = \dfrac{{12\sqrt 3 }}{{33}} \Rightarrow \alpha = 63,{16^o}\)
Hình bên là một bộ đèn chùm 10 bóng.
Biết \(S.ABCD\) là một hình chóp đều. Cảc cạnh bên là ba đoạn dây treo, \(AB = 44\;{\rm{cm}}\). Các cạnh đáy là ống thép tròn đều, \(BC = 68\;{\rm{cm}}\). Bộ đèn được treo lên trần nhà bởi đoạn dây \(SA\)
Biết tổng khối lượng của các cạnh và 9 bóng đèn là \(5\;{\rm{kg}}\), bỏ qua khối lượng của các dây \(AB,{\rm{ }}AC,{\rm{ }}AD\). Tính lực căng trên dây \(AB\).
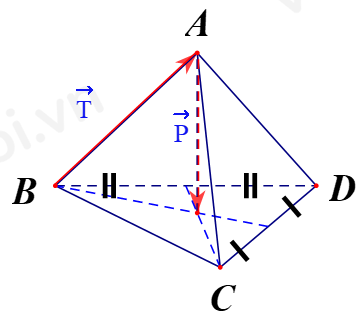
Ta gọi lực căng dây AB là \(T\), trọng lực tác động lên các cạnh của và 9 bóng đèn là P
Khi đó ta có:
\(\begin{array}{l}\cos \alpha = \sqrt {1 - {{\sin }^2}\alpha } = \dfrac{{\sqrt {73} }}{{11}}\\T = \dfrac{P}{{\cos \alpha }} = \dfrac{{5.9,8}}{{\dfrac{{\sqrt {73} }}{{11}}}} \approx 63,1\left( N \right)\end{array}\)
