Người ta trộn 2 loại quặng sắt với nhau, loại 1 chứa 72% sắt, loại 2 chứa 58% sắt được 1 loại quặng chứa 62% sắt. Nếu tăng khối lượng của mỗi loại quặng thêm 15 tấn thì được loại quặng chứa 63,25% sắt. Tìm khối lượng mỗi loại quặng đã trộn.
Gọi khối lượng quặng loại 1 đem trộn là \(x\) tấn, khối lượng quặng loại 2 đem trộn là \(y\) tấn \(\left( {x,\,\,y > 0} \right).\)
Khi trộn loại 1 chứa 72% sắt, loại 2 chứa 58% sắt được 1 loại quặng chứa 62% sắt nên ta có phương trình:
\(\begin{array}{l}\,\,\,\,\,\,\,72\% x + 58\% y = 62\% (x + y)\\ \Leftrightarrow 72x + 58y = 62x + 62y\\ \Leftrightarrow 10x - 4y = 0\\ \Leftrightarrow 5x - 2y = 0\begin{array}{*{20}{c}}{}&{(1)}\end{array}\end{array}\)
Khi tăng khối lượng của mỗi loại quặng thêm 15 tấn thì được loại quặng chứa 63,25% sắt nên ta có:
\(\begin{array}{l}\,\,\,\,\,\,\,\,72\% (x + 15) + 58\% (y + 15) = 63,25\% (x + y + 30)\\ \Leftrightarrow 72x + 72.15 + 58y + 58.15 = 63,25x + 63,25y + 63,25.30\\ \Leftrightarrow 8,75x - 5,25y = - 52,5\\ \Leftrightarrow 5x - 3y = - 30\begin{array}{*{20}{c}}{}&{(2)}\end{array}\end{array}\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}5x - 2y = 0\\5x - 3y = - 30\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}y = 30\\5x - 3y = - 30\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 12\,\,\,\left( {tm} \right)\\y = 30\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy khối lượng quặng loại 1 đem trộn là 12 tấn, khối lượng quặng loại 2 đem trộn là 30 tấn.
Người ta cho thêm 1 kg nước vào dung dịch A thì được dung dịch B có nồng độ axit là 20%. Sau đó lại cho thêm 1 kg axit vào dung dịch B thì được dung dịch C có nồng độ axit là \(\dfrac{{100}}{3}\% \). Tính nồng độ axit trong dung dịch A.
Gọi khối lượng axit trong dung dịch A là là \(x;\) khối lượng nước trong dung dịch A là \(y\,\,\left( {kg,\,\,x,\,\,y > 0} \right).\)
Người ta cho thêm 1 kg nước vào dung dịch A thì được dung dịch B có nồng độ axit là 20% nên ta có:
\(\dfrac{x}{{x + y + 1}} = 20\% \Leftrightarrow 0.8x - 02y = 0,2\begin{array}{*{20}{c}}{}&{(1)}\end{array}\)
Lại cho thêm 1 kg axit vào dung dịch B thì được dung dịch C có nồng độ axit là \(\dfrac{{100}}{3}\% \) nên ta có:
\(\begin{array}{l}\dfrac{{x + 1}}{{x + y + 2}} = \dfrac{{100}}{3}\% \Leftrightarrow \dfrac{{x + 1}}{{x + y + 2}} = \dfrac{1}{3}\\ \Leftrightarrow 2x - y = - 1\begin{array}{*{20}{c}}{}&{(2)}\end{array}\end{array}\)
Từ (1) và (2) ta có hệ phương trình: \(\left\{ \begin{array}{l}0,8x - 0,2y = 0,2\\2x - y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x - y = 1\\2x - y = - 1\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}2x = 2\\2x - y = - 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 1\,\,\,\left( {tm} \right)\\y = 3\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy nồng độ axit trong dung dịch A là : \(\dfrac{1}{{3 + 1}}.100\% = 25\% .\)
Bạn Nam mua hai món hàng và phải trả tổng cộng 480000 đồng, trong đó đã tính cả 40000 đồng là thuế giá trị gia tăng (viết tắt là thuế VAT). Biết rằng thuế VAT đối với mặt hàng thứ nhất là 10%, thuế VAT đối với mặt hàng thứ hai là 8%. Hỏi nếu không kể thuế VAT thì bạn Nam phải trả mỗi món hàng là bao nhiêu tiền?
(Trong đó: Thuế VAT là thuế mà người mua hàng phải trả, người bán hàng thu và nộp cho Nhà nước. Giả sử thuế VAT đối với mặt hàng A được quy là 10%. Khi đó nếu giá bán của mặt hàng A là x đồng thì kể cả thuế VAT, người mua phải trả tổng cộng là \(x + 10\% x\) đồng).
Gọi số phải trả cho món hàng thứ nhất không kể thuế VAT là \(x\) đồng, \(\left( {0 < x < 480000} \right).\)
Gọi số phải trả cho món hàng thứ nhất không kể thuế VAT là \(y\) đồng, \(\left( {0 < y < 480000} \right).\)
Số tiền phải trả cho hai món hàng không mất thuế là: \(x + y = 480000 - 40000 = 440000.\;\;\;\;\left( 1 \right)\)
Số tiền thuế phải trả cho món hàng thứ nhất là: \(x.10\% = \dfrac{x}{{10}}\) (đồng)
Số tiền thuế phải trả cho món hàng thứ hai là: \(y.8\% = \dfrac{{2y}}{{25}}\) (đồng).
Số tiền thuế phải trả cho hai món hàng là: \(\dfrac{x}{{10}} + \dfrac{{2y}}{{25}} = 40000 \Leftrightarrow 5x + 4y = 2000000\;\;\;\;\;\left( 2 \right).\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + y = 440000\\5x + 4y = 2000000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 4y = 1760000\\5x + 4y = 2000000\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 240000\;\;\;\left( {tm} \right)\\y = 200000\;\;\;\left( {tm} \right)\end{array} \right..\)
Vậy số tiền phải trả cho món hàng thứ nhất không phải thuế là 240 000 đồng, món hàng thứ hai là 200 000 đồng.
Hai đại biểu của trường A và trường B tham dự một buổi hội thảo. Mỗi đại biểu của trường A lân lượt bắt tay với từng đại biểu của trường B một lần. Tính số đại biểu của mỗi trường, biết số cái bắt tay bằng ba lần tổng số đại biểu của cả hai trường và số đại biểu của trường A nhiều hơn số đại biểu của trường B.
Gọi số đại biểu của trường A là \(x\) (đại biểu) và số đại biểu của trường B là \(y\) (đại biểu) \(\left( {x,y \in \mathbb{N}^*;x > y} \right)\).
Mỗi đại biểu của trường A bắt tay với lần lượt từng đại biểu của trường B nên số cái bắt tay là \(xy\).
Vì số cái bắt tay bằng 3 lần tổng số đại biểu của cả hai trường nên \(xy = 3\left( {x + y} \right)\)
\( \Rightarrow xy = 3x + 3y \Leftrightarrow x\left( {y - 3} \right) = 3y\)
TH1: \(y = 3 \Leftrightarrow x.0 = 9\) (vô lí)
TH2: \(y \ne 3 \Rightarrow y = \dfrac{{3y}}{{y - 3}} = \dfrac{{3y - 9 + 9}}{{y - 3}} = 3 + \dfrac{9}{{y - 3}}\)
Do \(x \in \mathbb{N}^* \Rightarrow y - 3 \in Ư\left( 9 \right) = \left\{ { \pm 1; \pm 3; \pm 9} \right\}\)
Ta có bảng sau:
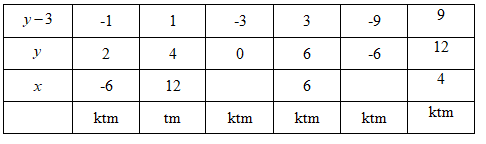
Vậy số đại biểu của trường A là 12 đại biểu và số đại biểu của trường B là 4 đại biểu.
Bạn N tiết kiệm bằng cách mỗi ngày bỏ tiền vào heo đất và chỉ dùng hai loại tiền giấy là tờ \(1000\) đồng và \(2000\) đồng. Hưởng ứng đợt vận động ủng hộ đồng bào bị lụt, bão nên N đập heo đất thu được \(160\,000\) đồng. Khi đó mẹ cho thêm bạn N số tờ tiền loại \(1000\) và số tờ tiền loại \(2000\) đồng lần lượt gấp 2 lần và 3 lần số tờ tiền cùng loại của bạn N có do tiết kiệm, vì vậy bạn N đã ủng hộ được tổng số tiền là \(560\,000\) đồng. Tính số tờ tiền mỗi loại của bạn N có do tiết kiệm.
Gọi \(x,y\) lần lượt là số tờ tiền mệnh giá \(1000\) và \(2000\) đồng mà bạn N có do tiết kiệm \(\left( {x,y \in {\rm N}*} \right).\)
Vì N để dành được \(160\,000\) nên ta có phương trình: \(1000x + 2000y = 160\,000\, \Rightarrow x + 2y = 160\,\,\,\left( 1 \right)\)
Sau khi mẹ cho N thêm, ta có:
+) Số tờ tiền mệnh giá \(1000\) đồng là: \(x + 2x = 3x\) đồng.
+) Số tờ mệnh giá \(2000\)đồng là: \(y + 3y = 4y\) đồng.
Do số tiền N ủng hộ là \(560\,000\) đồng nên ta có phương trình:
\(1000.3x + 2000.4y = 560\,000\)\( \Rightarrow 3x + 8y = 560\,\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{ \begin{array}{l}x + 2y = 160\\3x + 8y = 560\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}4x + 8y = 640\\3x + 8y = 560\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}x = 80\\80 + 2y = 160\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x = 80\,\,\,\left( {tm} \right)\\y = 40\,\,\,\left( {tm} \right)\end{array} \right.\)
Vậy số tờ tiền mệnh giá \(1000\) đồng là \(80\) và mệnh giá\(2000\) đồng là \(40.\)
