Bài tập ôn tập chương 6

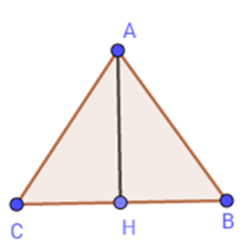
Cạnh của tam giác đều là: \(AB = BC = CA = 18:3 = 6(cm)\)

Gọi $AH$ là đường cao kẻ từ đỉnh $A$ của tam giác $ABC.$

Khi đó $AH$ vừa là đường cao vừa là đường trung tuyến của tam giác đều $ABC.$

Suy ra \(BH = HC = \dfrac{1}{2}BC = \dfrac{1}{2}.6 = 3(cm)\)

Áp dụng định lí Py-ta-go trong tam giác vuông $AHB$ ta có:

\(AH = \sqrt {A{B^2} - B{H^2}}  = \sqrt {{6^2} - {3^2}}  = \sqrt {27}  = 3\sqrt 3 (cm)\)

Diện tích tam giác đều là: \({S_{ABC}} = \dfrac{{AH.BC}}{2} = \dfrac{{3\sqrt 3 .6}}{2} = 9\sqrt 3 (c{m^2})\)

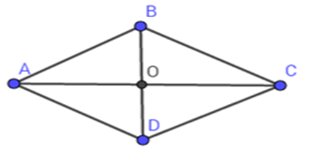
Ta có:

 \(AC = 2AO = 2.12 = 24cm\)

\(\begin{array}{l}{S_{ABCD}} = \dfrac{1}{2}BD.AC \Rightarrow BD = \dfrac{{2{S_{ABCD}}}}{{AC}} = \dfrac{{2.168}}{{24}} = 14(cm)\\ \Rightarrow BO = \dfrac{1}{2}BD = \dfrac{1}{2}.14 = 7(cm)\end{array}\)

Áp dụng định lí Py-ta-go trong tam giác vuông AOB vuông tại O ta có:

\(AB = \sqrt {A{O^2} + B{O^2}}  = \sqrt {{{12}^2} + {7^2}}  = \sqrt {193} (cm)\)

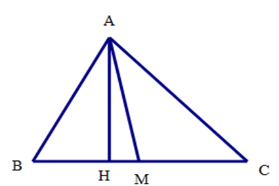
Ta có \({S_{ABM}} = \dfrac{1}{2}AH.BM\) ; \({S_{AMC}} = \dfrac{1}{2}AH.MC\) ; \({S_{ABC}} = \dfrac{1}{2}AH.BC\)

Mà \(M\) là trung điểm của \(BC\) nên \(MB = MC = \dfrac{{BC}}{2}\)

Từ đó ta suy ra \({S_{ABM}} = \dfrac{1}{2}AH.BM = \dfrac{1}{2}AH.CM = \dfrac{1}{2}AH.\dfrac{1}{2}BC = \dfrac{1}{2}\dfrac{{AH.BC}}{2}\)

Hay \({S_{ABM}} = {S_{ACM}} = \dfrac{1}{2}{S_{ABC}}\) .

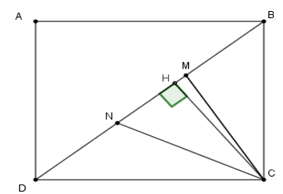
+ Ta có \(CD = AB = 9cm;BC = AD = 8cm\)  nên \({S_{BCD}} = \dfrac{1}{2}BC.DC = \dfrac{1}{2}.8.9 = 36\,c{m^2}\)

+ Kẻ \(CH \bot BD\) tại \(H.\)

+ Ta có \({S_{BCD}} = \dfrac{1}{2}CH.BD;{S_{CMN}} = \dfrac{1}{2}CH.MN\)  mà \(MN = \dfrac{1}{3}BD \Rightarrow {S_{CMN}} = \dfrac{1}{3}{S_{BCD}} = \dfrac{1}{3}.36 = 12\,c{m^2}\)

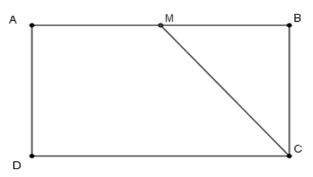
Ta có \({S_{ABCD}} = AB.BC\) ; \({S_{MBC}} = \dfrac{1}{2}MB.BC\)

Để \({S_{MBC}} = \dfrac{1}{4}{S_{ABCD}} \Leftrightarrow \dfrac{1}{2}MB.BC = \dfrac{1}{4}AB.BC\)\( \Leftrightarrow MB = \dfrac{1}{2}AB\)

Mà \(M \in AB\) nên \(M\) là trung điểm đoạn \(AB.\)

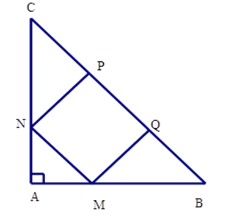
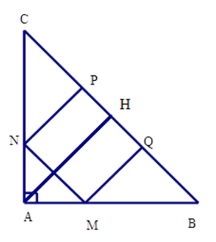
Ta có

Kẻ \(AH \bot BC \Rightarrow H\) là trung điểm cạnh \(BC\)  (vì tam giác \(ABC\) vuông cân tại \(A\) )

Khi đó \(AH\) là đường trung tuyến nên \(AH = \dfrac{{BC}}{2}\)  (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

+ Xét tam giác vuông \(CNP\) có \(\widehat C = 45^\circ \)  (do tam giác \(ABC\) vuông cân) nên tam giác \(CNP\) vuông cân tại \(P.\) Suy ra \(CP = PN = 22cm\)

+ Tương tự ta có \(\Delta QMB\) vuông cân tại \(Q \Rightarrow QM = QB = 22cm\)

Từ đó \(BC = PC + PQ + QB = 22 + 22 + 22 = 66cm\)

Mà \(AH = \dfrac{{BC}}{2}\left( {cmt} \right) \Rightarrow AH = \dfrac{{66}}{2} = 33cm\)

Từ đó \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.33.66 = 1089\,c{m^2}\)

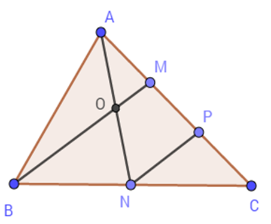
Lấy $P$ là trung điểm của $CM.$ Vì \(AM = \dfrac{1}{3}AC \Rightarrow MC = \dfrac{2}{3}AC \)\(\Rightarrow MP = PC = \dfrac{1}{3}AC = AM\)

Tam giác $BCM$ có: \(\left\{ \begin{array}{l}NB = NC\,\,(gt)\\PC = PM\,\,(gt)\end{array} \right.\)

Suy ra $NP$ là đường trung bình của tam giác $BMC$ (định nghĩa).

Suy ra \(NP//BM\)  (tính chất đường trung bình).

Tam giác ANP có  \(\left\{ \begin{array}{l}MA = MP\,\,\,(cmt)\\OM//NP\,\,\,(do\,\,NP//BM)\end{array} \right.\)

\( \Rightarrow AO = ON\) (định lý đảo của đường trung bình).

Theo chứng minh trên ta có OM là đường trung bình của tam giác ANP nên \(OM = \dfrac{1}{2}NP\,\,\,\,(1)\)

NP là đường trung bình của tam giác BCM nên \(NP = \dfrac{1}{2}BM\,\,\,(2)\)

Từ (1) và (2) suy ra \(BM = 4OM \Rightarrow BO = 3OM\) .

Vậy cả A, B đều đúng.

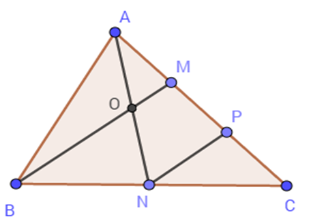
Hai tam giác $AOM$ và $ABM$ có chung đường cao hạ từ $A$ nên  \(\dfrac{{{S_{AOM}}}}{{{S_{ABM}}}} = \dfrac{{OM}}{{BM}} \)\(= \dfrac{1}{4} \Rightarrow {S_{AOM}} = \dfrac{1}{4}{S_{ABM}}\)

Hai tam giác $ABM$ và $ABC$ có chung đường cao hạ từ $B$ nên \(\dfrac{{{S_{ABM}}}}{{{S_{ABC}}}} = \dfrac{{AM}}{{AC}} = \dfrac{1}{3} \)\(\Rightarrow {S_{ABM}} = \dfrac{1}{3}{S_{ABC}}\)

Vậy \({S_{AOM}} = \dfrac{1}{4}.\dfrac{1}{3}.12 = 1\left( {c{m^2}} \right)\)

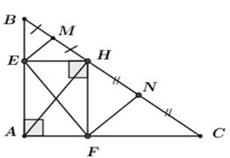
Áp dụng định lý Pi-ta-go trong tam giác $ABC$ vuông tại $A$ ta có:

\(BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{6^2} + {8^2}}  = \sqrt {100}  = 10\,cm.\)

 Áp dụng định lý Pi-ta-go trong tam giác $ABH$ vuông tại $H$ ta có:

\(A{H^2} = A{B^2} - B{H^2} = 36 - B{H^2}.\) 

Áp dụng định lý Pi-ta-go trong tam giác $ACH$ vuông tại $H$ ta có:

\(\begin{array}{l}A{H^2} = A{C^2} - H{C^2} = 64 - H{C^2}.\\ \Rightarrow 36 - B{H^2} = 64 - H{C^2}\\ \Leftrightarrow 36 - B{H^2} = 64 - {\left( {10 - BH} \right)^2}\\\left( {do\,\,\,HC + BH = BC = 10} \right)\\ \Leftrightarrow 28 - 100 + 20BH - B{H^2} + B{H^2} = 0\\ \Leftrightarrow 20BH = 72\\ \Leftrightarrow BH = 3,6\,\,\,cm.\\ \Rightarrow AH = \sqrt {36 - B{H^2}}  = \sqrt {36 - 3,{6^2}}  = 4,8\,\,cm.\end{array}\)

Xét tứ giác $AEHF$ có: \(\widehat A = \widehat E = \widehat F = {90^0}\,\,\,\left( {gt} \right)\)

\( \Rightarrow AEHF\) là hình chữ nhật (dhnb) \( \Rightarrow AH = EF\,\,\,\) (hai đường chéo hình chữ nhật bằng nhau).

\( \Rightarrow EF = AH = 4,8\,\,cm.\) 

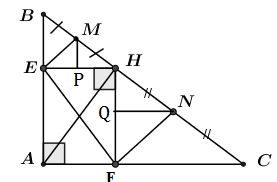
Kẻ \(MP \bot EH\,\,\left( {P \in EH} \right),\,\,NQ \bot HF\,\,\left( {Q \in HF} \right)\) ta có: MP và NQ lần lượt là đường trung bình của tam giác HBE và HFC nên \(MP = \dfrac{1}{2}BE,\,\,NQ = \dfrac{1}{2}FC\)

\(\begin{array}{l}{S_{\Delta MEH}} = \dfrac{1}{2}MP.EH = \dfrac{1}{2}.\dfrac{1}{2}BE.EH = \dfrac{1}{2}{S_{\Delta HBE}}\\{S_{\Delta HNF}} = \dfrac{1}{2}NQ.HF = \dfrac{1}{2}.\dfrac{1}{2}CF.HF = \dfrac{1}{2}{S_{\Delta HCF}}\\{S_{\Delta H{\rm{EF}}}} = \dfrac{1}{2}{S_{AEHF}}\\ \Rightarrow {S_{EMNF}} = \dfrac{1}{2}\left( {{S_{\Delta HBE}} + {S_{\Delta HCF}} + {S_{AEHF}}} \right) \\= \dfrac{1}{2}{S_{\Delta ABC}} = \dfrac{1}{2}\,.\dfrac{1}{2}.AB.AC = \dfrac{1}{4}.6.8 = 12\,\,\left( {c{m^2}} \right).\end{array}\)

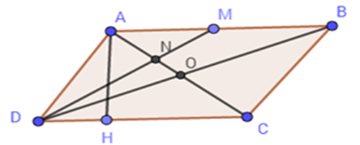
+) \({S_{ABCD}} = AH.CD = 4.3 = 12\left( {c{m^2}} \right)\)

+) Vì $M$ là trung điểm của $AB$ nên \(AM = \dfrac{1}{2}AB = \dfrac{1}{2}.4 = 2(cm)\)

Ta có chiều cao từ đỉnh $D$ đến cạnh $AM$ của tam giác $ADM$ bằng chiều cao $AH$ của hình bình hành.

\( \Rightarrow {S_{ADM}} = \dfrac{1}{2}AH.AM = \dfrac{1}{2}.3.2 = 3\left( {c{m^2}} \right)\)

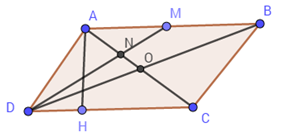
Tứ giác $ABCD$ là hình bình hành nên $AC$ và $BD$ cắt nhau tại trung điểm $O$ của mỗi đường.

Xét tam giác $ABD$ ta có: $AO$ và $DM$ là hai đường trung tuyến của tam giác.

Mà \(AO \cap DM = \left\{ N \right\} \Rightarrow \) $N$ là trọng tâm tam giác $ADB.$

\( \Rightarrow AN = \dfrac{2}{3}DM\) (tính chất đường trung tuyến của tam giác)

Suy ra  \(NM = \dfrac{{DM}}{3}\) .

+) Hai tam giác $AMN$ và $ADM$ có cùng đường cao hạ từ A nên \(\dfrac{{{S_{AMN}}}}{{{S_{ADM}}}} = \dfrac{{MN}}{{DM}} = \dfrac{1}{3}\)

Mà theo câu trước \({S_{\Delta ADM}} = 3\,c{m^2}\)

\( \Rightarrow {S_{AMN}} = \dfrac{1}{3}{S_{ADM}} = \dfrac{1}{3}.3 = 1\left( {c{m^2}} \right)\)

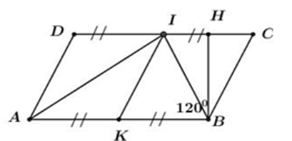
Kẻ $BH$ là đường cao ứng với cạnh $CD$ của hình bình hành $ABCD$\( \Rightarrow {S_{ABCD}} = BH.CD.\)

Theo đề bài ta có chu vi hình bình hành $ABCD$ bằng \(60cm.\)

\( \Rightarrow 2\left( {AB + BC} \right) = 60 \Leftrightarrow 2.3BC = 60 \Leftrightarrow BC = 10cm.\)

Xét tứ giác $KICB$ ta có: \(IC = BC = KB = IK = \dfrac{1}{2}AB=10cm\)

\( \Rightarrow IKBC\) là hình thoi. (dấu hiệu nhận biết).

Mà \(\widehat B = {120^0} \Rightarrow \widehat {ICB} = {180^0} - {120^0} = {60^0}.\)

Xét tam giác ICB có: \(\left\{ \begin{array}{l}IC = BC\\\widehat {ICB} = {60^0}\end{array} \right. \Rightarrow ICB\) là tam giác đều. (tam giác cân có góc ở đỉnh bằng \({60^0}\)).

\( \Rightarrow BH\) vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.

\( \Rightarrow HI = HC = \dfrac{1}{2}BC = 5cm.\)

Áp dụng định lý Pi-ta-go với tam giác vuông HBC ta có:

$BH = \sqrt {B{C^2} - H{C^2}}  = \sqrt {{{10}^2} - {5^2}}  = \sqrt {75}  = 5\sqrt 3 \,cm.$

$ \Rightarrow {S_{ABCD}} = BH.AB = BH.2BC = 5\sqrt 3 .2.10 = 100\sqrt 3 c{m^2}.$

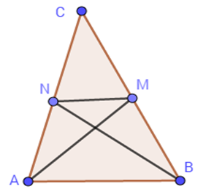
Ta có $ABMN$ là tứ giác có hai đường chéo $AM$ và $BN$ vuông góc nên có diện tích là: \({S_{ABMN}} = \dfrac{1}{2}AB.MN\)

Hai tam giác $AMC$ và $ABC$ có chung đường cao hạ từ $A$ nên \(\dfrac{{{S_{AMC}}}}{{{S_{ABC}}}} = \dfrac{{MC}}{{BC}} = \dfrac{1}{2}\)\( \Rightarrow {S_{AMC}} = \dfrac{1}{2}{S_{ABC}}\,(1)\)

Hai tam giác $AMN$ và $AMC$ có chung đường cao hạ từ $M$ nên \(\dfrac{{{S_{AMN}}}}{{{S_{AMC}}}} = \dfrac{{AN}}{{AC}} = \dfrac{1}{2}\)\( \Rightarrow {S_{AMN}} = \dfrac{1}{2}{S_{AMC}}\,(2)\)

Từ (1) và (2) suy ra \({S_{AMN}} = \dfrac{1}{4}{S_{ABC}}\,\)

Hai tam giác $AMB$ và $ABC$ có chung đường cao hạ từ $A$ nên \(\dfrac{{{S_{AMB}}}}{{{S_{ABC}}}} = \dfrac{{MB}}{{BC}} = \dfrac{1}{2}\)\( \Rightarrow {S_{AMB}} = \dfrac{1}{2}{S_{ABC}}\,\)

Ta có: \({S_{ABMN}} = {S_{AMN}} + {S_{ABM}} = \dfrac{1}{4}{S_{ABC}} + \dfrac{1}{2}{S_{ABC}} = \dfrac{3}{4}{S_{ABC}}\)

\( \Rightarrow {S_{ABC}} = \dfrac{4}{3}{S_{ABMN}} = \dfrac{4}{3}.\dfrac{1}{2}.AM.BN = \dfrac{2}{3}AM.BN\)