Câu hỏi:
2 năm trước
Cho tam giác $ABC$ có diện tích \(12c{m^2}\) . Gọi $N$ là trung điểm của $BC,{\rm{ }}M$ trên $AC$ sao cho \(AM = \dfrac{1}{3}AC\) , $AN$ cắt $BM$ tại $O$ .
Tính diện tích tam giác $AOM$
Trả lời bởi giáo viên
Đáp án đúng: d
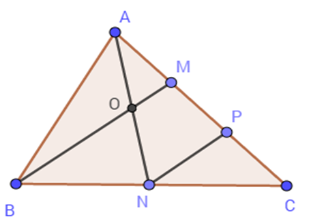
Hai tam giác $AOM$ và $ABM$ có chung đường cao hạ từ $A$ nên \(\dfrac{{{S_{AOM}}}}{{{S_{ABM}}}} = \dfrac{{OM}}{{BM}} \)\(= \dfrac{1}{4} \Rightarrow {S_{AOM}} = \dfrac{1}{4}{S_{ABM}}\)
Hai tam giác $ABM$ và $ABC$ có chung đường cao hạ từ $B$ nên \(\dfrac{{{S_{ABM}}}}{{{S_{ABC}}}} = \dfrac{{AM}}{{AC}} = \dfrac{1}{3} \)\(\Rightarrow {S_{ABM}} = \dfrac{1}{3}{S_{ABC}}\)
Vậy \({S_{AOM}} = \dfrac{1}{4}.\dfrac{1}{3}.12 = 1\left( {c{m^2}} \right)\)
Hướng dẫn giải:
+) Sử dụng công thức tính diện tích tam giác và tỉ lệ của diện tích các tam giác.

