Tính $BC$, $EF.$

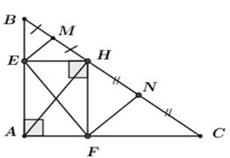
Áp dụng định lý Pi-ta-go trong tam giác $ABC$ vuông tại $A$ ta có:

$BC = \sqrt {A{B^2} + A{C^2}}  = \sqrt {{6^2} + {8^2}}  = \sqrt {100}  = 10\,cm.$

 Áp dụng định lý Pi-ta-go trong tam giác $ABH$ vuông tại $H$ ta có:

$A{H^2} = A{B^2} - B{H^2} = 36 - B{H^2}.$ 

Áp dụng định lý Pi-ta-go trong tam giác $ACH$ vuông tại $H$ ta có:

$\begin{array}{l}A{H^2} = A{C^2} - H{C^2} = 64 - H{C^2}.\\ \Rightarrow 36 - B{H^2} = 64 - H{C^2}\\ \Leftrightarrow 36 - B{H^2} = 64 - {\left( {10 - BH} \right)^2}\\\left( {do\,\,\,HC + BH = BC = 10} \right)\\ \Leftrightarrow 28 - 100 + 20BH - B{H^2} + B{H^2} = 0\\ \Leftrightarrow 20BH = 72\\ \Leftrightarrow BH = 3,6\,\,\,cm.\\ \Rightarrow AH = \sqrt {36 - B{H^2}}  = \sqrt {36 - 3,{6^2}}  = 4,8\,\,cm.\end{array}$

Xét tứ giác $AEHF$ có: $\widehat A = \widehat E = \widehat F = {90^0}\,\,\,\left( {gt} \right)$

$\Rightarrow AEHF$ là hình chữ nhật (dhnb) $\Rightarrow AH = EF\,\,\,$ (hai đường chéo hình chữ nhật bằng nhau).

$\Rightarrow EF = AH = 4,8\,\,cm.$