Tam giác $ABC$ có hai trung tuyến $AM$ và $BN$ vuông góc với nhau. Hãy tính diện tích tam giác đó theo hai cạnh $AM$ và $BN.$

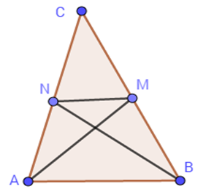
Ta có $ABMN$ là tứ giác có hai đường chéo $AM$ và $BN$ vuông góc nên có diện tích là: \({S_{ABMN}} = \dfrac{1}{2}AB.MN\)

Hai tam giác $AMC$ và $ABC$ có chung đường cao hạ từ $A$ nên \(\dfrac{{{S_{AMC}}}}{{{S_{ABC}}}} = \dfrac{{MC}}{{BC}} = \dfrac{1}{2}\)\( \Rightarrow {S_{AMC}} = \dfrac{1}{2}{S_{ABC}}\,(1)\)

Hai tam giác $AMN$ và $AMC$ có chung đường cao hạ từ $M$ nên \(\dfrac{{{S_{AMN}}}}{{{S_{AMC}}}} = \dfrac{{AN}}{{AC}} = \dfrac{1}{2}\)\( \Rightarrow {S_{AMN}} = \dfrac{1}{2}{S_{AMC}}\,(2)\)

Từ (1) và (2) suy ra \({S_{AMN}} = \dfrac{1}{4}{S_{ABC}}\,\)

Hai tam giác $AMB$ và $ABC$ có chung đường cao hạ từ $A$ nên \(\dfrac{{{S_{AMB}}}}{{{S_{ABC}}}} = \dfrac{{MB}}{{BC}} = \dfrac{1}{2}\)\( \Rightarrow {S_{AMB}} = \dfrac{1}{2}{S_{ABC}}\,\)

Ta có: \({S_{ABMN}} = {S_{AMN}} + {S_{ABM}} = \dfrac{1}{4}{S_{ABC}} + \dfrac{1}{2}{S_{ABC}} = \dfrac{3}{4}{S_{ABC}}\)

\( \Rightarrow {S_{ABC}} = \dfrac{4}{3}{S_{ABMN}} = \dfrac{4}{3}.\dfrac{1}{2}.AM.BN = \dfrac{2}{3}AM.BN\)