Trả lời bởi giáo viên
Đáp án đúng: b
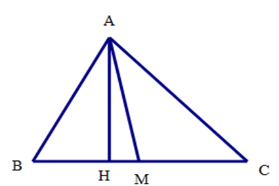
Ta có \({S_{ABM}} = \dfrac{1}{2}AH.BM\) ; \({S_{AMC}} = \dfrac{1}{2}AH.MC\) ; \({S_{ABC}} = \dfrac{1}{2}AH.BC\)
Mà \(M\) là trung điểm của \(BC\) nên \(MB = MC = \dfrac{{BC}}{2}\)
Từ đó ta suy ra \({S_{ABM}} = \dfrac{1}{2}AH.BM = \dfrac{1}{2}AH.CM = \dfrac{1}{2}AH.\dfrac{1}{2}BC = \dfrac{1}{2}\dfrac{{AH.BC}}{2}\)
Hay \({S_{ABM}} = {S_{ACM}} = \dfrac{1}{2}{S_{ABC}}\) .
Hướng dẫn giải:
Sử dụng công thức tính diện tích tam giác: \(S = \dfrac{1}{2}ah\) với \(a\) là độ dài đáy, \(h\) là độ dài chiều cao ứng với đáy.

