Cho hình bình hành $ABCD$ có \(\widehat B = {120^0},AB = 2BC.\) Gọi $I$ là trung điểm của $CD,{\rm{ }}K$ là trung điểm của $AB.$ Biết chu vi hình bình hành $ABCD$ bằng $60cm.$  Tính diện tích hình bình hành $ABCD.$

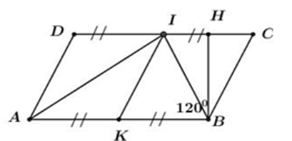
Kẻ $BH$ là đường cao ứng với cạnh $CD$ của hình bình hành $ABCD$\( \Rightarrow {S_{ABCD}} = BH.CD.\)

Theo đề bài ta có chu vi hình bình hành $ABCD$ bằng \(60cm.\)

\( \Rightarrow 2\left( {AB + BC} \right) = 60 \Leftrightarrow 2.3BC = 60 \Leftrightarrow BC = 10cm.\)

Xét tứ giác $KICB$ ta có: \(IC = BC = KB = IK = \dfrac{1}{2}AB=10cm\)

\( \Rightarrow IKBC\) là hình thoi. (dấu hiệu nhận biết).

Mà \(\widehat B = {120^0} \Rightarrow \widehat {ICB} = {180^0} - {120^0} = {60^0}.\)

Xét tam giác ICB có: \(\left\{ \begin{array}{l}IC = BC\\\widehat {ICB} = {60^0}\end{array} \right. \Rightarrow ICB\) là tam giác đều. (tam giác cân có góc ở đỉnh bằng \({60^0}\)).

\( \Rightarrow BH\) vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.

\( \Rightarrow HI = HC = \dfrac{1}{2}BC = 5cm.\)

Áp dụng định lý Pi-ta-go với tam giác vuông HBC ta có:

$BH = \sqrt {B{C^2} - H{C^2}}  = \sqrt {{{10}^2} - {5^2}}  = \sqrt {75}  = 5\sqrt 3 \,cm.$

$ \Rightarrow {S_{ABCD}} = BH.AB = BH.2BC = 5\sqrt 3 .2.10 = 100\sqrt 3 c{m^2}.$