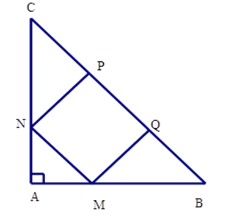
Cho hình vuông $MNPQ$ nội tiếp tam giác $ABC$ vuông cân tại $A$ (hình vẽ). Biết \({S_{MNPQ}} = 484c{m^2}.\;\) Tính \({S_{ABC}}\).

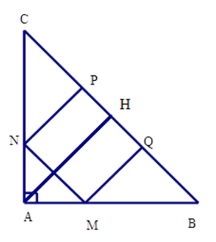
Ta có

Kẻ \(AH \bot BC \Rightarrow H\) là trung điểm cạnh \(BC\)  (vì tam giác \(ABC\) vuông cân tại \(A\) )

Khi đó \(AH\) là đường trung tuyến nên \(AH = \dfrac{{BC}}{2}\)  (tính chất đường trung tuyến ứng với cạnh huyền trong tam giác vuông)

+ Xét tam giác vuông \(CNP\) có \(\widehat C = 45^\circ \)  (do tam giác \(ABC\) vuông cân) nên tam giác \(CNP\) vuông cân tại \(P.\) Suy ra \(CP = PN = 22cm\)

+ Tương tự ta có \(\Delta QMB\) vuông cân tại \(Q \Rightarrow QM = QB = 22cm\)

Từ đó \(BC = PC + PQ + QB = 22 + 22 + 22 = 66cm\)

Mà \(AH = \dfrac{{BC}}{2}\left( {cmt} \right) \Rightarrow AH = \dfrac{{66}}{2} = 33cm\)

Từ đó \({S_{ABC}} = \dfrac{1}{2}AH.BC = \dfrac{1}{2}.33.66 = 1089\,c{m^2}\)