Câu hỏi:
3 năm trước
Tính diện tích của tam giác đều \(ABC\) biết chu vi tam giác \(ABC\) bằng $18cm.$
Trả lời bởi giáo viên
Đáp án đúng: c
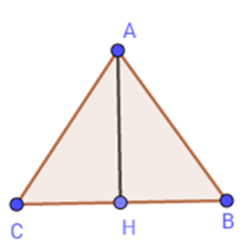
Cạnh của tam giác đều là: \(AB = BC = CA = 18:3 = 6(cm)\)
Gọi $AH$ là đường cao kẻ từ đỉnh $A$ của tam giác $ABC.$
Khi đó $AH$ vừa là đường cao vừa là đường trung tuyến của tam giác đều $ABC.$
Suy ra \(BH = HC = \dfrac{1}{2}BC = \dfrac{1}{2}.6 = 3(cm)\)
Áp dụng định lí Py-ta-go trong tam giác vuông $AHB$ ta có:
\(AH = \sqrt {A{B^2} - B{H^2}} = \sqrt {{6^2} - {3^2}} = \sqrt {27} = 3\sqrt 3 (cm)\)
Diện tích tam giác đều là: \({S_{ABC}} = \dfrac{{AH.BC}}{2} = \dfrac{{3\sqrt 3 .6}}{2} = 9\sqrt 3 (c{m^2})\)
Hướng dẫn giải:
Tính độ dài đường cao hạ từ đỉnh $A.$
Sử dụng công thức tính diện tích tam giác bằng nửa tích chiều cao với cạnh đáy tương ứng.

