Câu hỏi:
2 năm trước
Cho hình chữ nhật ABCD có \(AD = 8cm,\;AB = 9cm\). Các điểm $M,{\rm{ }}N$ trên đường chéo $BD$ sao cho $BM = MN = ND.$ Tính diện tích tam giác $CMN.$
Trả lời bởi giáo viên
Đáp án đúng: a
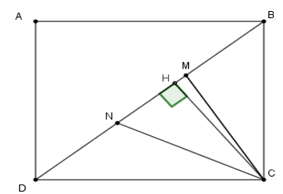
+ Ta có \(CD = AB = 9cm;BC = AD = 8cm\) nên \({S_{BCD}} = \dfrac{1}{2}BC.DC = \dfrac{1}{2}.8.9 = 36\,c{m^2}\)
+ Kẻ \(CH \bot BD\) tại \(H.\)
+ Ta có \({S_{BCD}} = \dfrac{1}{2}CH.BD;{S_{CMN}} = \dfrac{1}{2}CH.MN\) mà \(MN = \dfrac{1}{3}BD \Rightarrow {S_{CMN}} = \dfrac{1}{3}{S_{BCD}} = \dfrac{1}{3}.36 = 12\,c{m^2}\)
Hướng dẫn giải:
+ Tính tỉ số diện tích tam giác \(CMN\) và tam giác \(BCD\)
+ Tính diện tích \(\Delta BCD\) suy ra diện tích tam giác \(CMN.\)

