Cho tam giác \(ABC,\,\,\widehat A = {90^0},\,\,AB = 6cm,\,\,AC = 8cm.\) Hạ $AH \bot BC,$ qua \(H\) kẻ \(HE \bot AB,\,\,HF \bot AC\) với \(E \in AB;F \in AC\).
Gọi \(M,\,\,N\) lần lượt là trung điểm của \(HB\) và \(HC\). Tính diện tích tứ giác $MNFE$ .
Trả lời bởi giáo viên
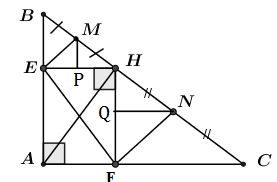
Kẻ \(MP \bot EH\,\,\left( {P \in EH} \right),\,\,NQ \bot HF\,\,\left( {Q \in HF} \right)\) ta có: MP và NQ lần lượt là đường trung bình của tam giác HBE và HFC nên \(MP = \dfrac{1}{2}BE,\,\,NQ = \dfrac{1}{2}FC\)
\(\begin{array}{l}{S_{\Delta MEH}} = \dfrac{1}{2}MP.EH = \dfrac{1}{2}.\dfrac{1}{2}BE.EH = \dfrac{1}{2}{S_{\Delta HBE}}\\{S_{\Delta HNF}} = \dfrac{1}{2}NQ.HF = \dfrac{1}{2}.\dfrac{1}{2}CF.HF = \dfrac{1}{2}{S_{\Delta HCF}}\\{S_{\Delta H{\rm{EF}}}} = \dfrac{1}{2}{S_{AEHF}}\\ \Rightarrow {S_{EMNF}} = \dfrac{1}{2}\left( {{S_{\Delta HBE}} + {S_{\Delta HCF}} + {S_{AEHF}}} \right) \\= \dfrac{1}{2}{S_{\Delta ABC}} = \dfrac{1}{2}\,.\dfrac{1}{2}.AB.AC = \dfrac{1}{4}.6.8 = 12\,\,\left( {c{m^2}} \right).\end{array}\)
Hướng dẫn giải:
+) Tính diện tích theo mối quan hệ \({S_{MNFE}} = {S_{\Delta MEH}} + {S_{\Delta HEF}} + {S_{\Delta NFH}}\)
Giải thích thêm:
Các em cũng có thể tính diện tích theo mối quan hệ \({S_{MNFE}} = {S_{\Delta ABC}} - {S_{\Delta MBE}} - {S_{\Delta NCF}} - {S_{\Delta AEF}}\)

