Cho tam giác $ABC$ có diện tích \(12c{m^2}\) . Gọi $N$ là trung điểm của $BC,{\rm{ }}M$ trên $AC$ sao cho \(AM = \dfrac{1}{3}AC\) , $AN$ cắt $BM$ tại $O$ .
Chọn câu đúng.
Trả lời bởi giáo viên
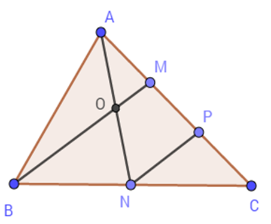
Lấy $P$ là trung điểm của $CM.$ Vì \(AM = \dfrac{1}{3}AC \Rightarrow MC = \dfrac{2}{3}AC \)\(\Rightarrow MP = PC = \dfrac{1}{3}AC = AM\)
Tam giác $BCM$ có: \(\left\{ \begin{array}{l}NB = NC\,\,(gt)\\PC = PM\,\,(gt)\end{array} \right.\)
Suy ra $NP$ là đường trung bình của tam giác $BMC$ (định nghĩa).
Suy ra \(NP//BM\) (tính chất đường trung bình).
Tam giác ANP có \(\left\{ \begin{array}{l}MA = MP\,\,\,(cmt)\\OM//NP\,\,\,(do\,\,NP//BM)\end{array} \right.\)
\( \Rightarrow AO = ON\) (định lý đảo của đường trung bình).
Theo chứng minh trên ta có OM là đường trung bình của tam giác ANP nên \(OM = \dfrac{1}{2}NP\,\,\,\,(1)\)
NP là đường trung bình của tam giác BCM nên \(NP = \dfrac{1}{2}BM\,\,\,(2)\)
Từ (1) và (2) suy ra \(BM = 4OM \Rightarrow BO = 3OM\) .
Vậy cả A, B đều đúng.
Hướng dẫn giải:
+) Sử dụng tính chất của đường trung bình trong tam giác.
+) Sử dụng tỉ lệ của diện tích các tam giác.

