Câu hỏi:
2 năm trước
Cho hình chữ nhật $ABCD$. Trên cạnh $AB$ lấy M . Tìm vị trí của M để \({S_{MBC}} = \dfrac{1}{4}{S_{ABCD}}\)
Trả lời bởi giáo viên
Đáp án đúng: c
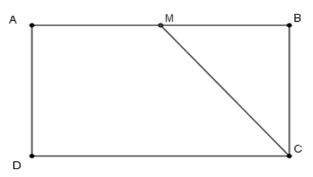
Ta có \({S_{ABCD}} = AB.BC\) ; \({S_{MBC}} = \dfrac{1}{2}MB.BC\)
Để \({S_{MBC}} = \dfrac{1}{4}{S_{ABCD}} \Leftrightarrow \dfrac{1}{2}MB.BC = \dfrac{1}{4}AB.BC\)\( \Leftrightarrow MB = \dfrac{1}{2}AB\)
Mà \(M \in AB\) nên \(M\) là trung điểm đoạn \(AB.\)
Hướng dẫn giải:
Sử dụng công thức tính diện tích hình chữ nhật và diện tích tam giác vuông.

