Tính các góc của hình thang $BDEC$ , biết $\widehat A = {70^o}$ .
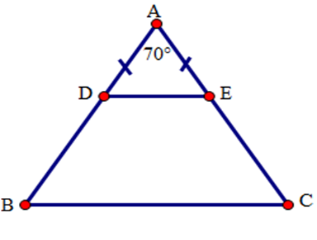
Ta có : \(\hat A = 70^\circ \)
Theo ý a) suy ra:
\(\widehat {ADE} = \widehat {AED} = \widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {DAE}} \right):2\;\)\( = (180^\circ - 70^\circ ):2 = 55^\circ \;\;\;\;\;\;\)
Vì \(\widehat {BDE}\) và \(\widehat {ADE}\) là hai góc kề bù nên \(\widehat {BDE} = 180^\circ - \widehat {ADE} = 180^\circ - 55^\circ = 125^\circ \)$ \Rightarrow \widehat {DEC} = 125^\circ $ (Vì $DEBC$ là hình thang cân)
Vậy \(\widehat {BDE} = \widehat {DEC} = 125^\circ ;\,\widehat {DBC} = \widehat {ECB} = 55^\circ \) .
Tứ giác $BDEC$ là hình gì?
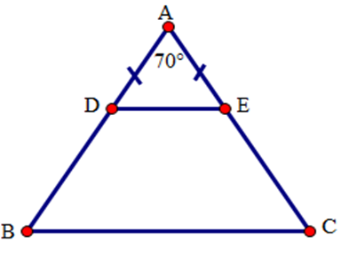
Tam giác $ADE$ có \(AD = AE(gt)\) nên tam giác $ADE$ cân tại $A$.
Suy ra \(\widehat {ADE} = \widehat {AED} = \left( {180^\circ - \widehat {DAE}} \right):2\;\left( 1 \right)\)
Tam giác $ABC$ cân tại $A$ (gt) nên \(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {BAC}} \right):2\;\;\;\;\left( 2 \right)\)
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ABC}\)
Mà 2 góc \(\widehat {ADE}\) và \(\widehat {ABC}\) là hai góc ở vị trí đồng vị nên suy ra $DE{\rm{//}}BC$
Tứ giác $BDEC$ có DE // BC nên tứ giác $BDEC$ là hình thang.
Lại có \(\widehat {ABC} = \widehat {ACB}\) (vì tam giác \(ABC\) cân tại \(A\) ) nên \(BDEC\) là hình thang cân.
Tứ giác $BDEC$ là hình gì?

Tam giác $ADE$ có \(AD = AE(gt)\) nên tam giác $ADE$ cân tại $A$.
Suy ra \(\widehat {ADE} = \widehat {AED} = \left( {180^\circ - \widehat {DAE}} \right):2\;\left( 1 \right)\)
Tam giác $ABC$ cân tại $A$ (gt) nên \(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {BAC}} \right):2\;\;\;\;\left( 2 \right)\)
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ABC}\)
Mà 2 góc \(\widehat {ADE}\) và \(\widehat {ABC}\) là hai góc ở vị trí đồng vị nên suy ra $DE{\rm{//}}BC$
Tứ giác $BDEC$ có DE // BC nên tứ giác $BDEC$ là hình thang.
Lại có \(\widehat {ABC} = \widehat {ACB}\) (vì tam giác \(ABC\) cân tại \(A\) ) nên \(BDEC\) là hình thang cân.
Chọn khẳng định đúng.
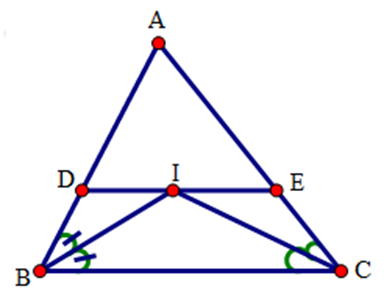
Vì $DE//BC$ (gt) nên suy ra \(\widehat {DIB} = \widehat {IBC}\) ( so le trong)
Mà \(\widehat {DBI} = \widehat {IBC}\) (gt) nên \(\widehat {DIB} = \widehat {DBI}\)
Suy ra tam giác $BDI$ cân đỉnh $D$.
Do đó \(DI = DB\,\,(1)\)
Ta có: $IE//CB$ nên suy ra \(\widehat {EIC} = \widehat {BCI}\) ( so le trong)
Mà \(\widehat {BCI} = \widehat {ECI}\) (gt) nên \(\widehat {ECI} = \widehat {EIC}\)
Suy ra tam giác $EIC$ cân đỉnh $E$.
Do đó \(EI = EC\,\,(2)\).
Cộng (1) và (2) vế theo vế ta được:
\(DI + EI = BD + CE \Rightarrow DE = BD + CE\)
Chọn khẳng định đúng nhất?
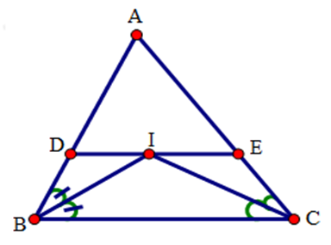
Xét tứ giác $DECB$ có: $DE//BC$ (gt) nên tứ giác $DECB$ là hình thang.
Tương tự :
Tứ giác $DICBS$ có $DI//BC$ (gt) nên tứ giác $DICB$ là hình thang
Tứ giác $IECB$ có $IE//CB$ (gt) nên tứ giác $IECB$ là hình thang.
Chọn khẳng định đúng nhất?

Xét tứ giác $DECB$ có: $DE//BC$ (gt) nên tứ giác $DECB$ là hình thang.
Tương tự :
Tứ giác $DICBS$ có $DI//BC$ (gt) nên tứ giác $DICB$ là hình thang
Tứ giác $IECB$ có $IE//CB$ (gt) nên tứ giác $IECB$ là hình thang.
Các điểm $M,N$ thỏa mãn điều kiện gì để $BM = MN = NC$ ?
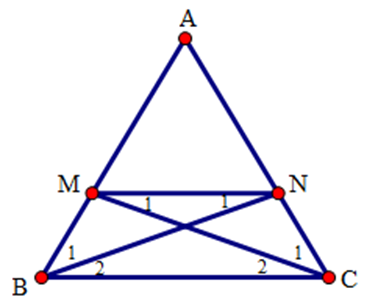
Ta có $BM = MN$ khi và chỉ khi \(\Delta MNB\) cân tại \(M \Rightarrow \) \(\widehat {{N_1}} = \widehat {{B_1}}\)\( \Leftrightarrow \widehat {{B_1}} = \widehat {{B_2}}\)(vì \(\widehat {{N_1}} = \widehat {{B_2}}\)) nên \(BN\) là phân giác góc $ABC$.
Tương tự $MN = NC$ khi và chỉ khi \(\Delta MNC\) cân tại \(N \Rightarrow \)\(\widehat {{C_1}} = \widehat {{C_2}}\) nên \(CM\) là phân giác góc \(ACB\) .
Như vậy, nếu $BN$ và $CM$ là các đường phân giác của tam giác $ABC$ thì $BM = MN = CN.$
Tứ giác $BMNC$ là hình gì?
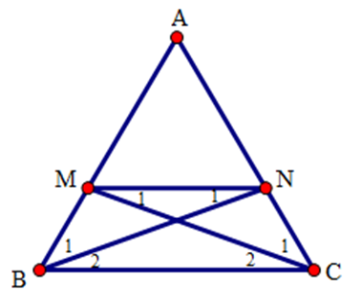
Ta có:$AB = AM + MB$ và $AC = AN + NC$ . Mà $AB = AC$ (do tam giác $ABC$ cân tại$A$ )và $BM = NC$ ( gt)
Suy ra $AN = AM$
Xét tam giác $AMN$ có: $AM = AN$ (cmt)
Suy ra tam giác $AMN$ cân tại$A$ . Suy ra \(\widehat {AMN} = \widehat {ANM}\)
Xét tam giác $ANM$ có: \(\widehat A + \widehat {AMN} + \widehat {ANM} = {180^0}\)(tổng ba góc trong một tam giác)
\(\widehat {AMN} = \dfrac{{{{180}^0} - \widehat A}}{2}\)( vì \(\widehat {AMN} = \widehat {ANM}\) ) (1)
Xét tam giác $ABC$ cân tại $A$ ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong một tam giác) nên $\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2}$ ( vì \(\widehat B = \widehat C\) ) (2)
Từ (1) và (2) \(\widehat {AMN} = \widehat B\)
Mà $\widehat {AMN},\widehat B$là hai góc đồng vị nên $MN$ //$BC$ .
Xét tứ giác $MNCB$ có $MN$ // $BC$ nên $MNCB$ là hình thang.
Lại có \(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại$A$ ) nên $MNCB$ là hình thang cân.
Tứ giác $BMNC$ là hình gì?

Ta có:$AB = AM + MB$ và $AC = AN + NC$ . Mà $AB = AC$ (do tam giác $ABC$ cân tại$A$ )và $BM = NC$ ( gt)
Suy ra $AN = AM$
Xét tam giác $AMN$ có: $AM = AN$ (cmt)
Suy ra tam giác $AMN$ cân tại$A$ . Suy ra \(\widehat {AMN} = \widehat {ANM}\)
Xét tam giác $ANM$ có: \(\widehat A + \widehat {AMN} + \widehat {ANM} = {180^0}\)(tổng ba góc trong một tam giác)
\(\widehat {AMN} = \dfrac{{{{180}^0} - \widehat A}}{2}\)( vì \(\widehat {AMN} = \widehat {ANM}\) ) (1)
Xét tam giác $ABC$ cân tại $A$ ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong một tam giác) nên $\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2}$ ( vì \(\widehat B = \widehat C\) ) (2)
Từ (1) và (2) \(\widehat {AMN} = \widehat B\)
Mà $\widehat {AMN},\widehat B$là hai góc đồng vị nên $MN$ //$BC$ .
Xét tứ giác $MNCB$ có $MN$ // $BC$ nên $MNCB$ là hình thang.
Lại có \(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại$A$ ) nên $MNCB$ là hình thang cân.
Tứ giác $BDEC$ là hình gì?

Tam giác $ADE$ có \(AD = AE(gt)\) nên tam giác $ADE$ cân tại $A$.
Suy ra \(\widehat {ADE} = \widehat {AED} = \left( {180^\circ - \widehat {DAE}} \right):2\;\left( 1 \right)\)
Tam giác $ABC$ cân tại $A$ (gt) nên \(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat {BAC}} \right):2\;\;\;\;\left( 2 \right)\)
Từ (1) và (2) suy ra \(\widehat {ADE} = \widehat {ABC}\)
Mà 2 góc \(\widehat {ADE}\) và \(\widehat {ABC}\) là hai góc ở vị trí đồng vị nên suy ra $DE{\rm{//}}BC$
Tứ giác $BDEC$ có DE // BC nên tứ giác $BDEC$ là hình thang.
Lại có \(\widehat {ABC} = \widehat {ACB}\) (vì tam giác \(ABC\) cân tại \(A\) ) nên \(BDEC\) là hình thang cân.
Chọn khẳng định đúng nhất?

Xét tứ giác $DECB$ có: $DE//BC$ (gt) nên tứ giác $DECB$ là hình thang.
Tương tự :
Tứ giác $DICBS$ có $DI//BC$ (gt) nên tứ giác $DICB$ là hình thang
Tứ giác $IECB$ có $IE//CB$ (gt) nên tứ giác $IECB$ là hình thang.
Tứ giác $BMNC$ là hình gì?

Ta có:$AB = AM + MB$ và $AC = AN + NC$ . Mà $AB = AC$ (do tam giác $ABC$ cân tại$A$ )và $BM = NC$ ( gt)
Suy ra $AN = AM$
Xét tam giác $AMN$ có: $AM = AN$ (cmt)
Suy ra tam giác $AMN$ cân tại$A$ . Suy ra \(\widehat {AMN} = \widehat {ANM}\)
Xét tam giác $ANM$ có: \(\widehat A + \widehat {AMN} + \widehat {ANM} = {180^0}\)(tổng ba góc trong một tam giác)
\(\widehat {AMN} = \dfrac{{{{180}^0} - \widehat A}}{2}\)( vì \(\widehat {AMN} = \widehat {ANM}\) ) (1)
Xét tam giác $ABC$ cân tại $A$ ta có: \(\widehat A + \widehat B + \widehat C = {180^0}\) (tổng ba góc trong một tam giác) nên $\widehat B = \dfrac{{{{180}^0} - \widehat A}}{2}$ ( vì \(\widehat B = \widehat C\) ) (2)
Từ (1) và (2) \(\widehat {AMN} = \widehat B\)
Mà $\widehat {AMN},\widehat B$là hai góc đồng vị nên $MN$ //$BC$ .
Xét tứ giác $MNCB$ có $MN$ // $BC$ nên $MNCB$ là hình thang.
Lại có \(\widehat B = \widehat C\) (\(\Delta ABC\) cân tại$A$ ) nên $MNCB$ là hình thang cân.
Câu nào sau đây là đúng khi nói về hình thang:
Theo định nghĩa: “Hình thang là tứ giác có hai cạnh đối song song” nên A đúng.
Hình thang \(ABCD\) có: \(\hat D = {70^0},\hat B = {65^0},\hat C = {115^0}\). Số đo góc \(\widehat A\) là:
Vì tổng các góc của một tứ giác bằng \(360^\circ \) nên \(\widehat A + \widehat B + \widehat C + \widehat D = 360^\circ \Rightarrow \widehat A = 360^\circ - 70^\circ - 65^\circ - 115^\circ = 110^\circ \).
Góc kề cạnh bên của hình thang có số đo là \({130^0}\). Góc kề còn lại của cạnh bên đó là:
Vì tổng hai góc kề cạnh bên của hình thang bằng \(180^\circ \) nên góc kề còn lại của cạnh bên đó có số đo bằng \(180^\circ - 130^\circ = 50^\circ \).
Cho tam giác \(\Delta AMN\) cân tại \(A.\) Các điểm \(B,C\) lần lượt trên các cạnh AM, AN sao cho \(AB = AC\). Hãy chọn câu đúng:
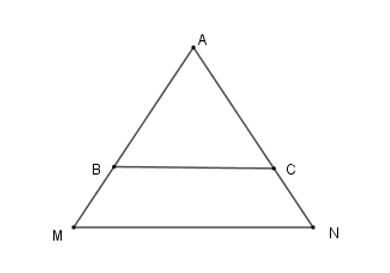
Xét \(\Delta BAC\) có: \(BA = CA(gt)\) nên \(\Delta BCA\) là tam giác cân.
Suy ra: \(\widehat {CBA} = \widehat {ABC} = \dfrac{{180^\circ - \widehat A}}{2}\) (1) nên A đúng.
Vì \(\Delta AMN\) cân tại \(A \Rightarrow AM = AN\) mà \(AB = AC\) nên \(AM - AB = AN - AC \Leftrightarrow MB = NC\) do dó C đúng.
Lại có: \(\widehat {ANM} = \widehat {AMN} = \dfrac{{180^\circ - \widehat A}}{2}\) (2) (do \(\Delta AMN\) cân tại \(A\)).
Từ (1) và (2) suy ra: \(\widehat {ABC} = \widehat {AMN}\)
Mà hai góc \(\widehat {ABC}\) và \(\widehat {AMN}\) là hai góc ở vị trí đồng vị nên suy ra \(BC//MN\).
Tứ giác \(BCNM\) có: \(MN//BC\) (cmt) nên là hình thang.
Hình thang \(BCNM\) có: \(\widehat {BMN} = \widehat {CNM}\,\left( {cmt} \right)\) nên là hình thang cân. Do đó, B đúng.
Vậy cả A, B, C đều đúng.
Cho hình thang \(ABCD\) có \(\hat A = \hat D = 90^\circ ,\;DC = BC = 2.AB\). Tính góc \(ABC\) của hình thang.
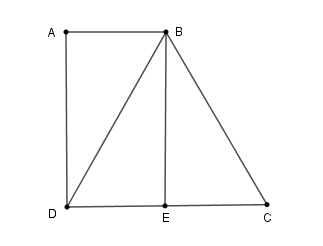
Từ \(B\) kẻ \(BE\) vuông góc với \(CD\) tại \(E.\)
Tứ giác \(ABED\) là hình thang có hai cạnh bên \(AD{\rm{//}}BE\) nên \(AD = BE,AB = DE\).
Mặt khác, \(DC = BC = 2AB\) nên \(DC = 2ED\), do đó \(E\) là trung điểm của \(DC\).
Xét \(\Delta BDE\) và \(\Delta BCE\) có \(\widehat {BED} = \widehat {BEC} = 90^\circ ;\,DE = EC;BE\) cạnh chung nên \(\Delta BED = \Delta BEC\left( {c - g - c} \right)\).
Suy ra \(BD = BC\) mà \(BC = DC\left( {gt} \right) \Rightarrow BD = BC = CD\) nên \(\Delta BCD\) đều.
Xét \(\Delta BCD\) đều có \(BE\) là đường cao cũng là đường phân giác nên \(\widehat {EBC} = \dfrac{1}{2}\widehat {DBC} = \dfrac{1}{2}60^\circ = 30^\circ \).
Vì \(AD//BE\) mà \(\widehat {BAD} = 90^\circ \) nên \(\widehat {ABE} = 180^\circ - \widehat {BAD} = 180^\circ - 90^\circ = 90^\circ \) (hai góc trong cũng phía bù nhau)
Từ đó \(\widehat {ABC} = \widehat {ABE} + \widehat {EBC} = 90^\circ + 30^\circ = 120^\circ \).
Vậy \(\widehat {ABC} = 120^\circ \).
Tính các góc của hình thang \(BEDC\), biết \(\widehat A = {80^o}\).
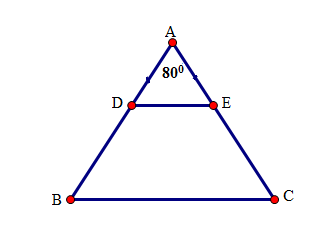
Ta có: \(\hat A = 80^\circ \)
Vì \(\Delta ABC\) cân tại \(A\) nên
\(\widehat {ABC} = \widehat {ACB} = \left( {180^\circ - \widehat A} \right):2\;\)\( = (180^\circ - 80^\circ ):2 = 50^\circ \;\;\;\;\;\;\).
Vì \(DE//BC\left( {gt} \right)\) nên \(\widehat {EDB} + \widehat {DBE} = 180^\circ \Leftrightarrow \widehat {BDE} = 180^\circ - 50^\circ = 130^\circ \).
Tương tự ta có: \(\widehat {DEC} = 130^\circ \)
Vậy \(\widehat {BDE} = \widehat {DEC} = 130^\circ ;\,\widehat {DBC} = \widehat {ECB} = 50^\circ \).
Chọn đáp án đúng nhất. Tứ giác \(BDEC\) là hình gì?
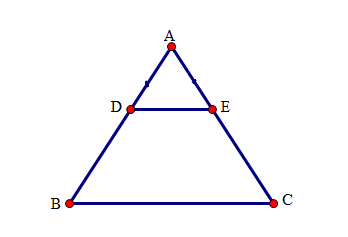
Tứ giác \(BDEC\) có DE // BC nên tứ giác \(BDEC\) là hình thang.
Lại có \(\widehat {ABC} = \widehat {ACB}\) (vì tam giác \(ABC\) cân tại \(A\) ) nên \(BDEC\) là hình thang cân.
Chọn đáp án đúng nhất. Tứ giác \(BDEC\) là hình gì?

Tứ giác \(BDEC\) có DE // BC nên tứ giác \(BDEC\) là hình thang.
Lại có \(\widehat {ABC} = \widehat {ACB}\) (vì tam giác \(ABC\) cân tại \(A\) ) nên \(BDEC\) là hình thang cân.

