Trả lời bởi giáo viên
Đáp án đúng: b
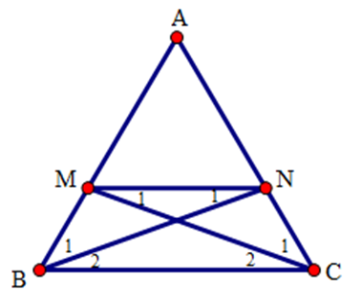
Ta có:AB=AM+MB và AC=AN+NC . Mà AB=AC (do tam giác ABC cân tạiA )và BM=NC ( gt)
Suy ra AN=AM
Xét tam giác AMN có: AM=AN (cmt)
Suy ra tam giác AMN cân tạiA . Suy ra ^AMN=^ANM
Xét tam giác ANM có: ˆA+^AMN+^ANM=1800(tổng ba góc trong một tam giác)
^AMN=1800−ˆA2( vì ^AMN=^ANM ) (1)
Xét tam giác ABC cân tại A ta có: ˆA+ˆB+ˆC=1800 (tổng ba góc trong một tam giác) nên ˆB=1800−ˆA2 ( vì ˆB=ˆC ) (2)
Từ (1) và (2) ^AMN=ˆB
Mà ^AMN,ˆBlà hai góc đồng vị nên MN //BC .
Xét tứ giác MNCB có MN // BC nên MNCB là hình thang.
Lại có ˆB=ˆC (ΔABC cân tạiA ) nên MNCB là hình thang cân.
Hướng dẫn giải:
Bước 1: Chứng minh MN//BC
Bước 2: Hình thang MNCB có hai góc ở đáy bằng nhau nên nó là hình thang cân.
