Câu hỏi:
2 năm trước
Cho tam giác \(\Delta AMN\) cân tại \(A.\) Các điểm \(B,C\) lần lượt trên các cạnh AM, AN sao cho \(AB = AC\). Hãy chọn câu đúng:
Trả lời bởi giáo viên
Đáp án đúng: d
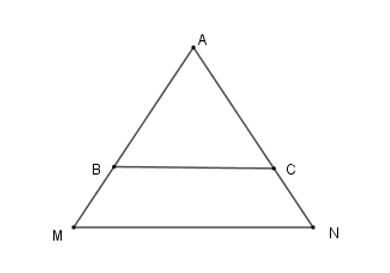
Xét \(\Delta BAC\) có: \(BA = CA(gt)\) nên \(\Delta BCA\) là tam giác cân.
Suy ra: \(\widehat {CBA} = \widehat {ABC} = \dfrac{{180^\circ - \widehat A}}{2}\) (1) nên A đúng.
Vì \(\Delta AMN\) cân tại \(A \Rightarrow AM = AN\) mà \(AB = AC\) nên \(AM - AB = AN - AC \Leftrightarrow MB = NC\) do dó C đúng.
Lại có: \(\widehat {ANM} = \widehat {AMN} = \dfrac{{180^\circ - \widehat A}}{2}\) (2) (do \(\Delta AMN\) cân tại \(A\)).
Từ (1) và (2) suy ra: \(\widehat {ABC} = \widehat {AMN}\)
Mà hai góc \(\widehat {ABC}\) và \(\widehat {AMN}\) là hai góc ở vị trí đồng vị nên suy ra \(BC//MN\).
Tứ giác \(BCNM\) có: \(MN//BC\) (cmt) nên là hình thang.
Hình thang \(BCNM\) có: \(\widehat {BMN} = \widehat {CNM}\,\left( {cmt} \right)\) nên là hình thang cân. Do đó, B đúng.
Vậy cả A, B, C đều đúng.
Hướng dẫn giải:
Sử dụng tính chất tam giác cân, định lý Ta-lét.
Tứ giác có hai cạnh đối song song là hình thang.
Hình thang có hai góc ở đáy bằng nhau là hình thang cân.
