Câu hỏi:
2 năm trước
Cho hình thang \(ABCD\) có \(\hat A = \hat D = 90^\circ ,\;DC = BC = 2.AB\). Tính góc \(ABC\) của hình thang.
Trả lời bởi giáo viên
Đáp án đúng: c
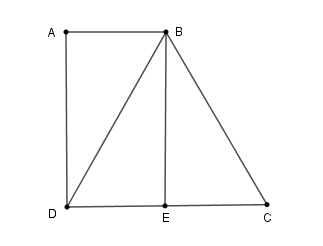
Từ \(B\) kẻ \(BE\) vuông góc với \(CD\) tại \(E.\)
Tứ giác \(ABED\) là hình thang có hai cạnh bên \(AD{\rm{//}}BE\) nên \(AD = BE,AB = DE\).
Mặt khác, \(DC = BC = 2AB\) nên \(DC = 2ED\), do đó \(E\) là trung điểm của \(DC\).
Xét \(\Delta BDE\) và \(\Delta BCE\) có \(\widehat {BED} = \widehat {BEC} = 90^\circ ;\,DE = EC;BE\) cạnh chung nên \(\Delta BED = \Delta BEC\left( {c - g - c} \right)\).
Suy ra \(BD = BC\) mà \(BC = DC\left( {gt} \right) \Rightarrow BD = BC = CD\) nên \(\Delta BCD\) đều.
Xét \(\Delta BCD\) đều có \(BE\) là đường cao cũng là đường phân giác nên \(\widehat {EBC} = \dfrac{1}{2}\widehat {DBC} = \dfrac{1}{2}60^\circ = 30^\circ \).
Vì \(AD//BE\) mà \(\widehat {BAD} = 90^\circ \) nên \(\widehat {ABE} = 180^\circ - \widehat {BAD} = 180^\circ - 90^\circ = 90^\circ \) (hai góc trong cũng phía bù nhau)
Từ đó \(\widehat {ABC} = \widehat {ABE} + \widehat {EBC} = 90^\circ + 30^\circ = 120^\circ \).
Vậy \(\widehat {ABC} = 120^\circ \).
Hướng dẫn giải:
Ta sử dụng tính chất hình thang, hình thang vuông.
Tính chất ha đường thẳng song song, tính chất tam giác đều.
