Hai mặt phẳng vuông góc

Gọi $H$ là trung điểm của $AB,$ tam giác $SAB$ đều $ \Rightarrow \,\,SH \bot AB.$

Mà $\left( {SAB} \right) \bot \left( {ABCD} \right)$$ \Rightarrow $$SH \bot \left( {ABCD} \right)$ và $SH = \dfrac{{a\sqrt 3 }}{2}$

Suy ra $\widehat {(SD;\left( {ABCD} \right))} = \widehat {\left( {SD;HD} \right)} = \widehat {SDH} = {30^0}$

Tam giác $SHD$ vuông tại $H,$ có $\tan \widehat {SDH} = \dfrac{{SH}}{{HD}} \Rightarrow HD = \dfrac{{3a}}{2}.$

Tam giác $AHD$ vuông tại $A,$ có $AD = \sqrt {H{D^2} - A{H^2}}  = a\sqrt 2 .$

Vậy diện tích hình chữ nhật $ABCD$ là ${S_{ABCD}} = \sqrt 2 \,{a^2}.$

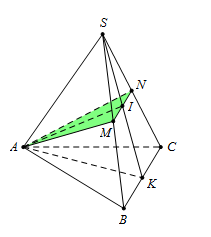
Gọi $K$ là trung điểm của $BC$ và $I = SK \cap MN$

Từ giả thiết $ \Rightarrow \,\,MN = \dfrac{1}{2}BC = \dfrac{a}{2},$ $MN\parallel BC$$ \Rightarrow \,\,I$ là trung điểm của $SK$ và $BC.$

Ta có $\Delta \,SAB = \Delta \,SAC$$ \Rightarrow $ Hai trung tuyến tương ứng $AM = AN.$

$ \Rightarrow \,\,\Delta \,AMN$ cân tại $A$$ \Rightarrow \,\,AI \bot MN.$ Mà $\left( {SBC} \right) \bot \left( {AMN} \right) \Rightarrow AI \bot \left( {SBC} \right)$

$ \Rightarrow \,\,AI \bot SK.$

Suy ra tam giác $SAK$ cân tại $A\,\, \Rightarrow \,\,SA = AK = \dfrac{{a\sqrt 3 }}{2}.$

Khi đó $S{K^2} = S{B^2} - B{K^2} = \dfrac{{{a^2}}}{2} \Rightarrow AI = \sqrt {S{A^2} - {{\left( {\dfrac{{SK}}{2}} \right)}^2}}  = \dfrac{{a\sqrt {10} }}{4}.$

Vậy diện tích tam giác $AMN$ là ${S_{\Delta \,AMN}} = \dfrac{1}{2}MN.AI = \dfrac{{{a^2}\sqrt {10} }}{{16}}.$

Gọi $I$ là trung điểm của $AB,$ tam giác $SAB$ đều $ \Rightarrow \,\,\left\{ \begin{array}{l}SI = \dfrac{{a\sqrt 3 }}{2}\\SI \bot AB\end{array} \right.$

Mà $\left( {SAB} \right) \bot \left( {ABC} \right)$$ \Rightarrow $$SI \bot \left( {ABC} \right)$; $\left\{ \begin{array}{l}SI \bot AC\\AB \bot AC\end{array} \right. \Rightarrow AC \bot \left( {SAB} \right).$

Kẻ $BK$ vuông góc với $SA$ tại $K,$ vì \(AC \bot \left( {SAB} \right)\) nên \(AC \bot BK \Rightarrow BK \bot \left( {SAC} \right)\) và $BK = \dfrac{{a\sqrt 3 }}{2}$

Do đó, góc giữa $BC$ và $mp\,\,\left( {SAC} \right)$ là $\widehat {BCK}\,\, \Rightarrow \,\,\widehat {BCK} = {30^0}.$

Khi đó $BC = \dfrac{{BK}}{{\sin \widehat {BCK}}} = a\sqrt 3  \Rightarrow AC = \sqrt {B{C^2} - A{B^2}}  = a\sqrt 2 .$

Vậy diện tích tam giác $ABC$ là ${S_{\Delta \,ABC}} = \dfrac{1}{2}.AB.AC = \dfrac{{{a^2}\sqrt 2 }}{2}.$

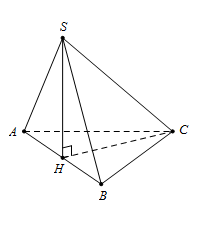
Gọi $H$ là trung điểm của $AB,$ tam giác $SAB$ cân tại $S \Rightarrow SH \bot AB.$

Mà $\left( {SAB} \right) \bot \left( {ABC} \right)$ nên $SH \bot \left( {ABC} \right)$ và đặt $SH = x.$

Tam giác $ABC$ vuông tại $A$ có $\left\{ \begin{array}{l}AB = BC.\sin C = a\\AC = BC.\cos C = a\sqrt 3 \end{array} \right..$

Ta có $SB = \sqrt {S{H^2} + H{B^2}}  = \sqrt {{x^2} + \dfrac{{{a^2}}}{4}} ,$ $HC = \sqrt {H{A^2} + A{C^2}}  = \dfrac{{a\sqrt {13} }}{2}$

Và $SC = \sqrt {S{H^2} + H{C^2}}  = \sqrt {{x^2} + \dfrac{{13{a^2}}}{4}} $

Tam giác SBC vuông tại S nên $S{B^2} + S{C^2} = B{C^2}$

$ \Leftrightarrow {x^2} + \dfrac{{{a^2}}}{4} + {x^2} + \dfrac{{13\,{a^2}}}{4} = 4{a^2} \Leftrightarrow {x^2} = \dfrac{{{a^2}}}{4}$$ \Leftrightarrow x = \dfrac{a}{2} \Rightarrow SH = \dfrac{a}{2}.$

Vậy diện tích tam giác $SAB$ là ${S_{\Delta \,SAB}} = \dfrac{1}{2}.SH.AB = \dfrac{{{a^2}}}{4}.$

Có vô số mặt phẳng qua A và vuông góc với \((P)\).

Hình lăng trụ đứng có đáy là hình chữ nhật là hình hộp chữ nhật nên có 6 mặt là hình chữ nhật.

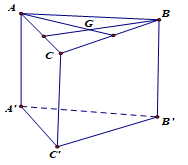
Do  ABC.A’B’C’ là hình lăng trụ tam giác đều  nên \(BB' \bot \left( {ABC} \right)\)

\( \Rightarrow BB' \bot AG\left( {AG \subset \left( {ABC} \right)} \right)\)

Do ABC là tam giác đều nên G vừa là trọng tâm vừa là trực tâm. Do đó:

\(\left. \begin{array}{l}AG \bot BC\\AG \bot B{B^\prime }\end{array} \right\} \Rightarrow AG \bot \left( {BC{C^\prime }{B^\prime }} \right)\)

\( \Rightarrow AG \bot {B^\prime }{C^\prime }\)

\(A{A^\prime } \bot (ABC)\) vì \(ABC \cdot {A^\prime }{B^\prime }{C^\prime }\) là hình lăng trụ đứng.