Trong các hình sau:

Các hình có thể là hình biểu diễn của một hình tứ diện là:
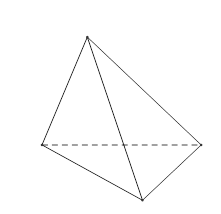
Hình (III) có thể là hình tứ diện. Vì nếu ta nhìn từ điểm C hướng xuống BD thì B, C, D thẳng hàng.
Hình (IV) có thể là hình tứ diện. Vì nếu điểm C nằm phía trước mặt phẳng (ABD) thì ta có thể nhìn thấy các đường CA,CB,CD, do đó các đường này là nét liền
Một hình chóp có đáy là ngũ giác có số mặt và số cạnh là :
Hình chóp ngũ giác có $5$ mặt bên + $1$ mặt đáy. $5$ cạnh bên và $5$ cạnh đáy.
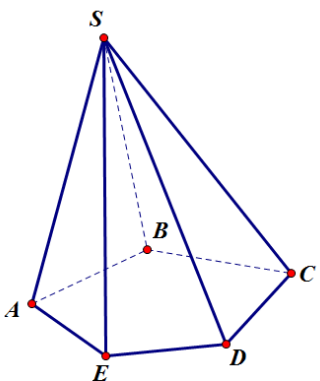
Trong các hình chóp, hình chóp có ít cạnh nhất có số cạnh là bao nhiêu?
Hình tứ diện là hình chóp có số cạnh ít nhất.
Chọn khẳng định sai trong các khẳng định sau?
Hai mặt phẳng có một điểm chung thì chúng có thể trùng nhau. Khi đó, chúng có vô số đường thẳng chung \( \Rightarrow \) B sai.
Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD{\rm{ }}\left( {AB\parallel CD} \right).\) Khẳng định nào sau đây sai?
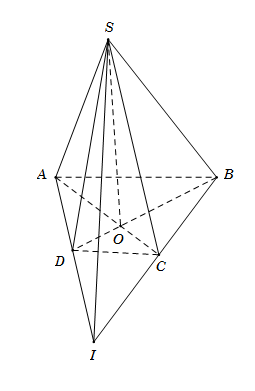
\( \bullet \) Hình chóp \(S.ABCD\) có 4 mặt bên: \(\left( {SAB} \right),\;\left( {SBC} \right),\;\left( {SCD} \right),\;\left( {SAD} \right).\) Do đó A đúng.
\( \bullet \) \(S\) là điểm chung thứ nhất của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right).\)
\(\left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\\O \in BD \subset \left( {SBD} \right) \Rightarrow O \in \left( {SBD} \right)\end{array} \right. \Rightarrow O\) là điểm chung thứ hai của hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBD} \right).\)
Do đó B đúng.
\( \bullet \) Tương tự, ta có \(\left( {SAD} \right) \cap \left( {SBC} \right) = SI.\) Do đó C đúng.
\( \bullet \) \(\left( {SAB} \right) \cap \left( {SAD} \right) = SA\) mà \(SA\) không phải là đường trung bình của hình thang \(ABCD.\) Do đó D sai.
Cho tứ diện \(ABCD.\) Gọi \(G\) là trọng tâm của tam giác\(BCD.\) Giao tuyến của mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right)\)là:
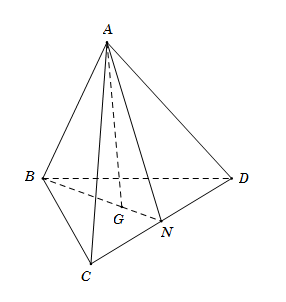
\( \bullet \) \(A\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)
\( \bullet \) Ta có:
\(BG \cap CD = N \Rightarrow \left\{ \begin{array}{l}N \in BG \subset \left( {ABG} \right) \Rightarrow N \in \left( {ABG} \right)\\N \in CD \subset \left( {ACD} \right) \Rightarrow N \in \left( {ACD} \right)\end{array} \right.\)
\( \Rightarrow N\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)
là điểm chung thứ hai giữa hai mặt phẳng \(\left( {ACD} \right)\) và \(\left( {GAB} \right).\)
Vậy \(\left( {ABG} \right) \cap \left( {ACD} \right) = AN.\)
Cho điểm $A$ không nằm trên mặt phẳng $\left( \alpha \right)$ chứa tam giác $BCD.$ Lấy $E,\,\,F$ là các điểm lần lượt nằm trên các cạnh $AB,\,\,AC.$ Khi $EF$ và $BC$ cắt nhau tại $I,$ thì $I$ không phải là điểm chung của hai mặt phẳng nào sau đây?
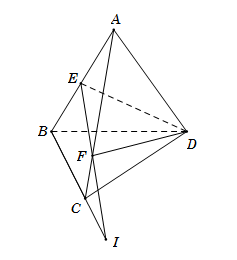
Điểm $I$ là giao điểm của $EF$ và $BC$ mà
\(\left\{ \begin{array}{l}BC \subset \left( {BCD} \right)\\EF \subset \left( {DEF} \right)\\EF \subset \left( {ABC} \right)\\EF \subset \left( {AEF} \right)\end{array} \right. \Rightarrow \left\{ \begin{array}{l}I \in \left( {BCD} \right) \cap \left( {DEF} \right)\\I \in \left( {BCD} \right) \cap \left( {ABC} \right)\\I \in \left( {BCD} \right) \cap \left( {AEF} \right)\end{array} \right.\)
Cho tứ diện \(ABCD.\) Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm của \(AC,{\rm{ }}CD.\) Giao tuyến của hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right)\) là:

\( \bullet \) \(B\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right).\)
\( \bullet \) Vì \(M,N\) lần lượt là trung điểm của \(AC,{\rm{ }}CD\) nên suy ra \(AN,{\rm{ }}DM\) là hai trung tuyến của tam giác \(ACD.\) Gọi \(G = AN \cap DM\)
\( \Rightarrow \left\{ \begin{array}{l}G \in AN \subset \left( {ABN} \right) \Rightarrow G \in \left( {ABN} \right)\\G \in DM \subset \left( {MBD} \right) \Rightarrow G \in \left( {MBD} \right)\end{array} \right. \Rightarrow G\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {MBD} \right)\) và \(\left( {ABN} \right).\)
Vậy \(\left( {ABN} \right) \cap \left( {MBD} \right) = BG.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(M,{\rm{ }}N\) lần lượt là trung điểm \(AD\) và \(BC.\) Giao tuyến của hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right)\) là:
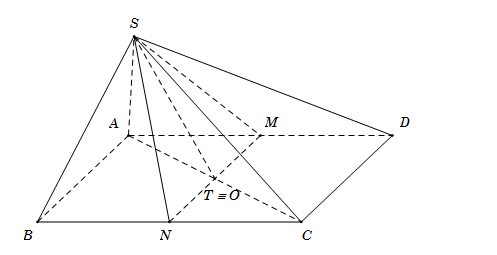
\( \bullet \) \(S\)là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right).\)
\( \bullet \) Gọi \(O = AC \cap BD\) là tâm của hình hình hành.
Trong mặt phẳng \(\left( {ABCD} \right)\) gọi \(T = AC \cap MN\) $ \Rightarrow T \equiv O$
\( \Rightarrow \left\{ \begin{array}{l}O \in AC \subset \left( {SAC} \right) \Rightarrow O \in \left( {SAC} \right)\\O \in MN \subset \left( {SMN} \right) \Rightarrow O \in \left( {SMN} \right)\end{array} \right. \)
\(\Rightarrow O\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {SMN} \right)\) và \(\left( {SAC} \right).\)
Vậy \(\left( {SMN} \right) \cap \left( {SAC} \right) = SO.\)
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình bình hành. Gọi \(I,{\rm{ }}J\) lần lượt là trung điểm \(SA,{\rm{ }}SB.\) Khẳng định nào sau đây sai?
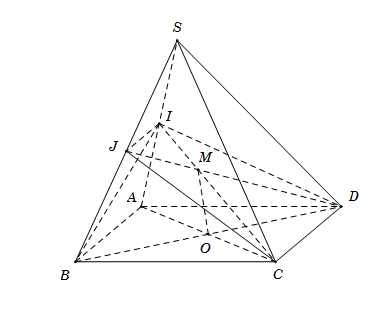
\( \bullet \) Ta có \(IJ\) là đường trung bình của tam giác \(SAB\) \( \Rightarrow IJ\parallel AB\parallel CD \Rightarrow IJ\parallel CD\)
\( \Rightarrow IJCD\) là hình thang. Do đó A đúng.
\( \bullet \) Ta có \(\left\{ \begin{array}{l}IB \subset \left( {SAB} \right)\\IB \subset \left( {IBC} \right)\end{array} \right. \Rightarrow \left( {SAB} \right) \cap \left( {IBC} \right) = IB.\) Do đó B đúng.
\( \bullet \) Ta có \(\left\{ \begin{array}{l}JD \subset \left( {SBD} \right)\\JD \subset \left( {JBD} \right)\end{array} \right. \Rightarrow \left( {SBD} \right) \cap \left( {JBD} \right) = JD.\) Do đó C đúng.
\( \bullet \) Trong mặt phẳng \(\left( {IJCD} \right)\), gọi \(M = IC \cap JD\)$ \Rightarrow \left( {IAC} \right) \cap \left( {JBD} \right) = MO.$ Do đó D sai.
Cho hình chóp \(S.ABCD\) có đáy là hình thang \(ABCD{\rm{ }}\left( {AD\parallel BC} \right).\) Gọi \(M\) là trung điểm \(CD.\) Giao tuyến của hai mặt phẳng \(\left( {MSB} \right)\) và \(\left( {SAC} \right)\) là:
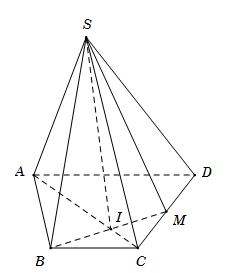
Gọi $I$ là giao điểm của $AC$ với $BM$
\( \bullet \) \(S\) là điểm chung thứ nhất giữa hai mặt phẳng \(\left( {MSB} \right)\) và \(\left( {SAC} \right).\)
\( \bullet \) Ta có \(\left\{ \begin{array}{l}I \in BM \subset \left( {SBM} \right) \Rightarrow I \in \left( {SBM} \right)\\I \in AC \subset \left( {SAC} \right) \Rightarrow I \in \left( {SAC} \right)\end{array} \right. \) \(\Rightarrow I\) là điểm chung thứ hai giữa hai mặt phẳng \(\left( {MSB} \right)\) và \(\left( {SAC} \right).\)
Vậy \(\left( {MSB} \right) \cap \left( {SAC} \right) = SI.\)
Cho 4 điểm không đồng phẳng $A,\,\,B,\,\,C,\,\,D.$ Gọi $I,\,\,K$ lần lượt là trung điểm của $AD$ và $BC.$ Giao tuyến của $\left( {IBC} \right)$ và $\left( {KAD} \right)$ là:
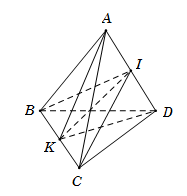
Điểm $K$ là trung điểm của $BC$ suy ra $K \in \left( {IBC} \right)\,\, \Rightarrow \,\,IK \subset \left( {IBC} \right).$
Điểm $I$ là trung điểm của $AD$ suy ra $I \in \left( {KAD} \right)\,\, \Rightarrow \,\,IK \subset \left( {KAD} \right).$
Vậy giao tuyến của hai mặt phẳng $\left( {IBC} \right)$ và $\left( {KAD} \right)$ là $IK.$
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang với \(AB\parallel CD\). Gọi \(I\) là giao điểm của \(AC\) và \(BD\). Trên cạnh \(SB\) lấy điểm \(M\). Tìm giao tuyến của hai mặt phẳng \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).
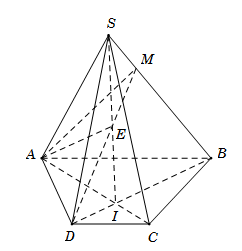
Ta có \(A\) là điểm chung thứ nhất của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).
Trong mặt phẳng \(\left( {SBD} \right)\), gọi \(E = SI \cap DM\).
Ta có:
● \(E \in SI\) mà \(SI \subset \left( {SAC} \right)\) suy ra \(E \in \left( {SAC} \right)\).
● \(E \in DM\) mà \(DM \subset \left( {ADM} \right)\) suy ra \(E \in \left( {ADM} \right)\).
Do đó \(E\) là điểm chung thứ hai của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).
Vậy $AE$ là giao tuyến của \(\left( {ADM} \right)\) và \(\left( {SAC} \right)\).
Cho tứ diện $ABCD$ và điểm $M$ thuộc miền trong của tam giác $ACD\,.$ Gọi $I$ và $J$ lần lượt là hai điểm trên cạnh $BC$ và $BD$ sao cho $IJ$ không song song với $CD\,.$ Gọi $H,\,\,K$ lần lượt là giao điểm của $IJ$ với $CD$, của $MH$ và $AC\,.$ Giao tuyến của hai mặt phẳng $\left( {ACD} \right)$ và $\left( {IJM} \right)$ là:
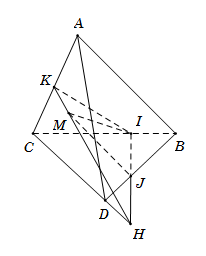
Trong mặt phẳng $\left( {BCD} \right),$ $IJ$ cắt $CD$ tại $H\,\, \Rightarrow \,\,H \in \left( {ACD} \right).$
Điểm $H \in IJ$ suy ra bốn điểm $M,\,\,I,\,\,J,\,\,H$ đồng phẳng.
Nên trong mặt phẳng $\left( {IJM} \right)$, $MH$ cắt $IJ$ tại $H$ và $MH \subset \left( {IJM} \right).$
Mặt khác $\left\{ \begin{array}{l}M \in \left( {ACD} \right)\\H \in \left( {ACD} \right)\end{array} \right.\,\, \Rightarrow \,\,MH \subset \left( {ACD} \right).$ Vậy $\left( {ACD} \right) \cap \left( {IJM} \right) = MH.$

