Trường hợp đồng dạng thứ nhất

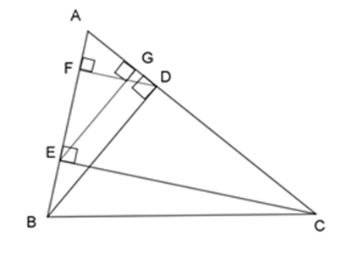
 Xét $\Delta ABD$ và $\Delta \;AEG$, ta có:

$BD \bot AC$ ($BD$ là đường cao)

$EG \bot AC$ ($EG$ là đường cao)

$\Rightarrow BD{\rm{//}}EG$

Theo định lý Talet, ta có:

$\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}$

$\Rightarrow$$\Delta AEG\backsim\Delta ABD$ (c - c -c) (điều phải chứng minh)

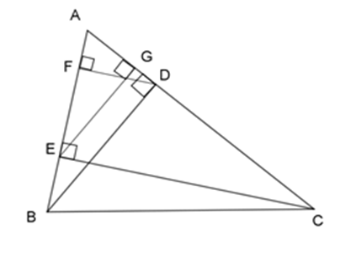
Từ câu trước  ta có:

$\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}}$$\Rightarrow AE.AD = AB.AG\;\;(1)$

Chứng minh tương tự, ta được:

$\Delta AFD$$\backsim$$\Delta AEC$ (c – c – c)

$\Rightarrow \dfrac{{AF}}{{AE}} = \dfrac{{AD}}{{AC}} \Rightarrow AF.AC = AE.AD\;\;(2)$

Từ (1) và (2) ta có:

$AD.AE = AB.AG = AC.AF$ .

 Xét $\Delta ABD$ và $\Delta \;AEG$, ta có:

$BD \bot AC$ ($BD$ là đường cao)

$EG \bot AC$ ($EG$ là đường cao)

$\Rightarrow BD{\rm{//}}EG$

Theo định lý Talet, ta có:

$\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}$

$\Rightarrow$$\Delta AEG\backsim\Delta ABD$ (c - c -c) (điều phải chứng minh)

 Xét $\Delta ABD$ và $\Delta \;AEG$, ta có:

$BD \bot AC$ ($BD$ là đường cao)

$EG \bot AC$ ($EG$ là đường cao)

$\Rightarrow BD{\rm{//}}EG$

Theo định lý Talet, ta có:

$\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}$

$\Rightarrow$$\Delta AEG\backsim\Delta ABD$ (c - c -c) (điều phải chứng minh)

Ta thấy $\dfrac{4}{{12}} = \dfrac{5}{{15}} = \dfrac{6}{{18}} = \dfrac{1}{3}$ nên A đúng.

$\dfrac{3}{9} = \dfrac{4}{{12}} \ne \dfrac{6}{{16}}$ nên B sai.

$\dfrac{2}{1} = \dfrac{2}{1} = \dfrac{2}{1}$ nên C đúng.

$\dfrac{{14}}{7} = \dfrac{{15}}{{7,5}} = \dfrac{{16}}{8} = 2$ nên D đúng.

$2$ tam giác $RSK$ và $PQM$ có: $\dfrac{{RS}}{{MP}} = \dfrac{{RK}}{{PQ}} = \dfrac{{KS}}{{MQ}}$, khi đó ta có: $\Delta RSK \backsim \Delta PMQ$.

Vì $\Delta ABC$ đồng dạng với $\Delta MNP$ nên $\dfrac{{AB}}{{MN}} = \dfrac{{AC}}{{MP}} = \dfrac{{BC}}{{NP}}$ hay

 $\dfrac{2}{6} = \dfrac{{AC}}{6} = \dfrac{3}{{NP}}$$\Rightarrow AC = \dfrac{{2.6}}{6} = 2;NP = \dfrac{{6.3}}{2} = 9$

Vậy $NP = 9cm,AC = 2cm$ nên A, B đúng.

Tam giác $ABC$ cân tại $A$, $\Delta MNP$ cân tại $M$ nên C đúng, D sai.

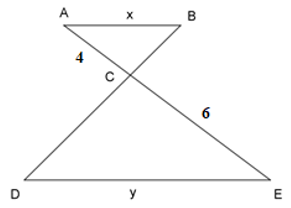
Ta có: $\Delta ABC\backsim\Delta EDC$

$\Rightarrow \dfrac{{AB}}{{ED}} = \dfrac{{AC}}{{EC}} \Leftrightarrow \dfrac{x}{y} = \dfrac{4}{6} = \dfrac{2}{3}$.

Vì $\Delta DEF$$\backsim$$\Delta ABC$ theo tỉ số ${k_1},$$\Delta MNP$$\backsim$$\Delta DEF$ theo tỉ số ${k_2}$ nên ta có: $\dfrac{{DE}}{{AB}} = {k_1} \Rightarrow AB = \dfrac{{DE}}{{{k_1}}}$  và$\dfrac{{MN}}{{DE}} = {k_2} \Rightarrow MN = {k_2}.DE$.

Từ đó ta có: $\dfrac{{AB}}{{MN}} = \dfrac{{\dfrac{{DE}}{{{k_1}}}}}{{{k_2}.DE}} = \dfrac{{\dfrac{1}{{{k_1}}}}}{{{k_2}}} = \dfrac{1}{{{k_1}{k_2}}}$.

Vì $\Delta ABC$$\backsim$$\Delta IKH$ nên $\dfrac{{AB}}{{IK}} = \dfrac{{BC}}{{KH}} = \dfrac{{AC}}{{IH}}$  hay $\dfrac{{IK}}{{AB}} = \dfrac{{KH}}{{BC}} = \dfrac{{IH}}{{AC}}$ nên (I) và (II) đúng, (III) sai.

Do đó chỉ có $1$ khẳng định sai.

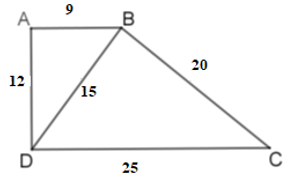
Ta có: $\dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{{BD}}{{DC}}$ (vì $\dfrac{9}{{15}} = \dfrac{{12}}{{20}} = \dfrac{{15}}{{25}}\,\left( { = \dfrac{3}{3}} \right)$).

Suy ra $\Delta ABD\backsim\Delta BDC\,\left( {c - c - c} \right)$

$\Delta ABD\backsim\Delta BDC$ nên $\widehat {ABD} = \widehat {BDC}.$ Mà hai góc này ở vị trí so le trong nên $AB$ //$CD$. Vậy $ABCD$ là hình thang.

Lại có: $B{D^2} = 225 = A{D^2} + A{B^2}$ nên $\Delta ABD$ vuông tại $A$. Do đó $ABCD$ là hình thang vuông.

Vậy A, B, C đều đúng, D sai.

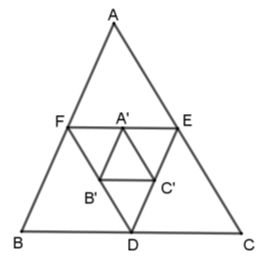
Vì $D,E,F$ theo thứ tự là trung điểm của $BC,CA,AB$ nên $EF;\,ED;\,FD$ là các đường trung bình của tam giác $ABC$ nên $\dfrac{{EF}}{{BC}} = \dfrac{{FD}}{{AC}} = \dfrac{{ED}}{{AB}} = \dfrac{1}{2}$ suy ra $\Delta EDF \backsim \Delta ABC\left( {c - c - c} \right)$ theo tỉ số đồng dạng $k = \dfrac{1}{2}$ hay (I) đúng.

Tương tự ta có $A'B';\,B'C';\,C'A'$ là các đường trung bình của tam giác $DEF$ nên $\Delta A'B'C'\backsim\Delta DEF$ theo tỉ số $k = \dfrac{1}{2}$ nên (III) sai.

Theo tính chất đường trung bình $\dfrac{{B'C'}}{{EF}} = \dfrac{1}{2}$ mà $\dfrac{{EF}}{{BC}} = \dfrac{1}{2}$ (cmt) suy ra $\dfrac{{B'C'}}{{BC}} = \dfrac{1}{4}.$

Tương tự $\dfrac{{A'B'}}{{AB}} = \dfrac{{A'C'}}{{AC}} = \dfrac{1}{4}.$

Do đó $\Delta A'B'C'\backsim\Delta ABC\,\left( {c - c - c} \right)$ theo tỉ số $k = \dfrac{1}{4}$ hay (II) đúng.

Do đó có $2$ khẳng định đúng.

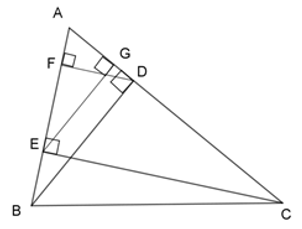
Từ câu trước  ta có:

$\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}$$\Rightarrow AE.AD = AB.AG\;\;(1)$ nên A đúng.

Chứng minh tương tự, ta được:

$\Delta AFD\backsim\Delta AEC$ (c – c – c)

$\Rightarrow \dfrac{{AF}}{{AE}} = \dfrac{{AD}}{{AC}} = \dfrac{{FD}}{{EC}}$$\Rightarrow AF.AC = AE.AD\;\;(2)$ nên B đúng.

Ngoài ra $\dfrac{{AD}}{{AC}} = \dfrac{{FD}}{{EC}}$ $\Rightarrow AD.EC = AC.FD$ nên C đúng.

Chỉ có đáp án D sai vì $\dfrac{{AE}}{{EG}} = \dfrac{{AB}}{{BD}}$.

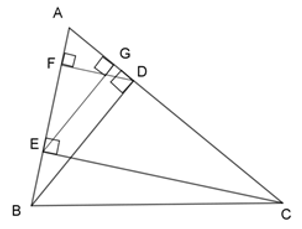
Xét $\Delta ABD$ và $\Delta AEG$, ta có:

$BD \bot AC$ (BD là đường cao)

$EG \bot AC$ (EG là đường cao)

$\Rightarrow BD{\rm{//}}EG$

Theo định lý Talet, ta có:

$\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}$

$\Rightarrow$$\Delta \;AEG\backsim\Delta ABD$ (c - c -c) nên (1) đúng.

Tương tự ta cũng chứng minh được $\Delta ADF \backsim \Delta ACE$ nên (2) đúng.

Dễ thấy (3) sai vì $\dfrac{{AE}}{{AB}} \ne \dfrac{{AC}}{{AC}}$.

Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.

Xét $\Delta ABD$ và $\Delta AEG$, ta có:

$BD \bot AC$ (BD là đường cao)

$EG \bot AC$ (EG là đường cao)

$\Rightarrow BD{\rm{//}}EG$

Theo định lý Talet, ta có:

$\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}$

$\Rightarrow$$\Delta \;AEG\backsim\Delta ABD$ (c - c -c) nên (1) đúng.

Tương tự ta cũng chứng minh được $\Delta ADF \backsim \Delta ACE$ nên (2) đúng.

Dễ thấy (3) sai vì $\dfrac{{AE}}{{AB}} \ne \dfrac{{AC}}{{AC}}$.

Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.

Tam giác thứ nhất có các cạnh là $12 < x < y$

Tam giác thứ hai có các cạnh là $x < y < 40,5$ .

Vì hai tam giác đồng dạng nên $\dfrac{{12}}{x} = \dfrac{x}{y} = \dfrac{y}{{40,5}}$ ta có: $xy = 12.40,5$ và ${x^2} = 12y$

Do đó ${x^2} = 12y = 12 \cdot \dfrac{{12.40,5}}{x}$ nên ${x^3} = 12.12.40,5 = {18^3}$$\Leftrightarrow x = 18$.

Suy ra $y = \dfrac{{12.40,5}}{{18}} = 27$.

Vậy $x = 18,y = 27$ $\Rightarrow S = 18 + 27 = 45$.

Ta thấy $\dfrac{4}{{12}} = \dfrac{5}{{15}} = \dfrac{6}{{18}} = \dfrac{1}{3}$ ; $\dfrac{3}{9} = \dfrac{4}{{12}} = \dfrac{6}{{18}} = \dfrac{1}{3}$  và $\dfrac{{14}}{7} = \dfrac{{15}}{{7,5}} = \dfrac{{16}}{8} = 2$; $\dfrac{{1,5}}{2} \ne \dfrac{2}{1} = \dfrac{2}{1}$ nên C sai.

2 tam giác RSK và PQM có $\dfrac{{RS}}{{PQ}} = \dfrac{{RK}}{{PM}} = \dfrac{{SK}}{{QM}}$, khi đó ta có:$\Delta RSK\;\; \backsim \;\;\Delta PQM$

Vì $\Delta ABC$ đồng dạng với $\Delta MNP$ nên $\dfrac{{AB}}{{MN}} = \dfrac{{AC}}{{MP}} = \dfrac{{BC}}{{NP}}$  hay

 $\begin{array}{l}\dfrac{5}{{10}} = \dfrac{{AC}}{5} = \dfrac{6}{{NP}}\\ \Rightarrow AC = \dfrac{{5.5}}{{10}} = 2,5;\,NP = \dfrac{{6.10}}{5} = 12\end{array}$

Vậy $NP = 12cm,AC = 2,5cm$.

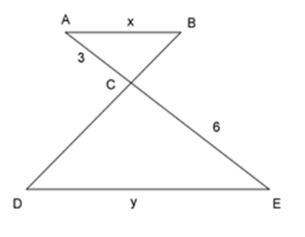
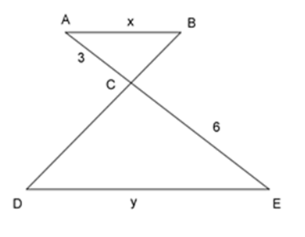
Ta có: $\Delta ABC\backsim\Delta EDC$

$\Rightarrow \dfrac{{AB}}{{ED}} = \dfrac{{AC}}{{EC}} \Leftrightarrow \dfrac{x}{y} = \dfrac{3}{6} = \dfrac{1}{2}$