\(\Delta ABC\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_1},\) \(\Delta MNP\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_2}.\) \(\Delta ABC\)\(\backsim\)$\Delta MNP$ theo tỉ số nào?
Vì \(\Delta ABC\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_1},\) \(\Delta MNP\)\(\backsim\)$\Delta DEF$ theo tỉ số \({k_2}\) nên ta có \(\dfrac{{AB}}{{DE}} = {k_1} \Rightarrow AB = {k_1}.DE\) và \(\dfrac{{MN}}{{DE}} = {k_2} \Rightarrow MN = {k_2}.DE\).
Từ đó ta có \(\dfrac{{AB}}{{MN}} = \dfrac{{{k_1}.DE}}{{{k_2}.DE}} = \dfrac{{{k_1}}}{{{k_2}}}.\)
Cho \(\Delta ABC\)\(\backsim\)\(\Delta IKH\). Có bao nhiêu khẳng định đúng trong các khẳng định sau:
(I) \(\dfrac{{HI}}{{AC}} = \dfrac{{KH}}{{BC}} = \dfrac{{KI}}{{AB}};\)
(II) \(\dfrac{{AB}}{{IK}} = \dfrac{{AC}}{{HI}} = \dfrac{{BC}}{{KH}};\)
(III) \(\dfrac{{AC}}{{IH}} = \dfrac{{AB}}{{KI}} = \dfrac{{BC}}{{IK}}.\)
Vì \(\Delta ABC\)\(\backsim\)\(\Delta IKH\) nên \(\dfrac{{AB}}{{IK}} = \dfrac{{BC}}{{KH}} = \dfrac{{AC}}{{IH}}\) hay \(\dfrac{{IK}}{{AB}} = \dfrac{{KH}}{{BC}} = \dfrac{{IH}}{{AC}}\) nên (I) và (II) đúng, (III) sai.
Tứ giác $ABCD$ có $AB = 8\,cm,BC = 15\,cm,CD = 18\,cm,AD = 10\,cm,BD = 12\,cm.$
Chọn câu đúng nhất:
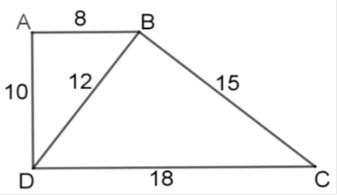
Ta có \(\dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{{BD}}{{DC}}\) (vì \(\dfrac{8}{{12}} = \dfrac{{10}}{{15}} = \dfrac{{12}}{{18}}\,\left( { = \dfrac{2}{3}} \right)\) )
nên \(\Delta ABD\)\(\backsim\) \(\Delta BDC\,\left( {c - c - c} \right)\)
\(\Delta ABD\)\(\backsim\)\(\Delta BDC\)nên \(\widehat {ABD} = \widehat {BDC}.\) Mà hai góc này ở vị trí so le trong nên $AB$ //$CD$ . Vậy $ABCD$ là hình thang.
Lại có \(B{D^2} = 144 < 164 = A{D^2} + A{B^2}\) nên \(\Delta ABD\) không vuông. Do đó \(ABCD\) không là hình thang vuông.
Vậy A, B đều đúng, C sai.
Cho tam giác $ABC$ . Các điểm $D,E,F$ theo thứ tự là trung điểm của $BC,CA,AB$ . Các điểm $A',B',C'$ theo thứ tự là trung điểm của $EF,DF,DE$ . Chọn câu đúng?
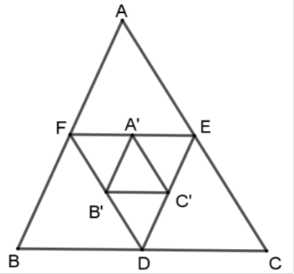
Vì $D,E,F$ theo thứ tự là trung điểm của $BC,CA,AB$ nên \(EF;\,ED;\,FD\) là các đường trung bình của tam giác \(ABC\) nên \(\dfrac{{EF}}{{BC}} = \dfrac{{FD}}{{AC}} = \dfrac{{ED}}{{AB}} = \dfrac{1}{2}\) suy ra \(\Delta ABC\backsim\Delta DEF\,\left( {c - c - c} \right)\) theo tỉ số đồng dạng \(k =2\) .
Tương tự ta có \(A'B';\,B'C';\,C'A'\) là các đường trung bình của tam giác \(DEF\) nên \(\Delta A'B'C'\)\(\backsim\)\(\Delta DEF\) theo tỉ số \(k = \dfrac{1}{2}\)
Theo tính chất đường trung bình $\dfrac{{B'C'}}{{EF}} = \dfrac{1}{2}$ mà $\dfrac{{EF}}{{BC}} = \dfrac{1}{2}$ (cmt) suy ra \(\dfrac{{B'C'}}{{BC}} = \dfrac{1}{4}.\)
Tương tự \(\dfrac{{A'B'}}{{AB}} = \dfrac{{A'C'}}{{AC}} = \dfrac{1}{4}.\)
Do đó \(\Delta A'B'C'\)\(\backsim\)\(\Delta ABC\,\left( {c - c - c} \right)\) theo tỉ số \(k = \dfrac{1}{4}\).
Cho \(\Delta ABC\) nhọn, kẻ đường cao $BD$ và $CE$ , vẽ các đường cao $DF$ và $EG$ của \(\Delta \;ADE\).
\(\Delta ABD\) đồng dạng với tam giác nào dưới đây?
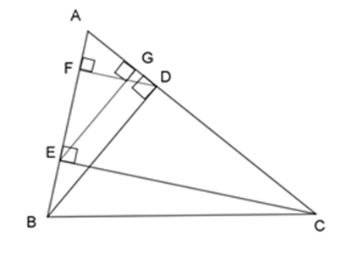
Xét \(\Delta ABD\) và $\Delta \;AEG$, ta có:
\(BD \bot AC\) ($BD$ là đường cao)
\(EG \bot AC\) ($EG$ là đường cao)
\( \Rightarrow BD{\rm{//}}EG\)
Theo định lý Talet, ta có:
\(\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}\)
\( \Rightarrow \)$\Delta AEG\backsim\Delta ABD$ (c - c -c) (điều phải chứng minh)
Cho \(\Delta ABC\) nhọn, kẻ đường cao $BD$ và $CE$ , vẽ các đường cao $DF$ và $EG$ của \(\Delta \;ADE\).
Chọn khẳng định đúng?
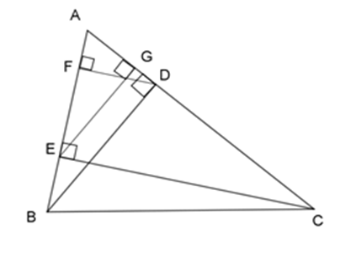
Từ câu trước ta có:
\(\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}}\)\( \Rightarrow AE.AD = AB.AG\;\;(1)\)
Chứng minh tương tự, ta được:
$\Delta AFD$$ \backsim $$\Delta AEC$ (c – c – c)
$ \Rightarrow \dfrac{{AF}}{{AE}} = \dfrac{{AD}}{{AC}} \Rightarrow AF.AC = AE.AD\;\;(2)$
Từ (1) và (2) ta có:
$AD.AE = AB.AG = AC.AF$ .
Một tam giác có cạnh nhỏ nhất bằng $8$ , hai cạnh còn lại bằng $x$ và $y$ \(\left( {x < y} \right).\) Một tam giác khác có cạnh lớn nhất bằng $27$ , hai cạnh còn lại cũng bằng $x$ và $y$ . Tính $x$ và $y$ để hai tam giác đó đồng dạng.
Tam giác thứ nhất có các cạnh là \(8 < x < y\)
Tam giác thứ hai có các cạnh là $x < y < 27$ .
Vì hai tam giác đồng dạng nên \(\dfrac{8}{x} = \dfrac{x}{y} = \dfrac{y}{{27}}\) ta có \(x.y = 8.27\) và \({x^2} = 8y.\)
Do đó \({x^2} = 8y = 8 \cdot \dfrac{{8.27}}{x}\)nên \({x^3} = 64.27 = {\left( {4.3} \right)^3}.\)
Vậy \(x = 12,y = 18.\)

