Câu hỏi:
2 năm trước
Cho \(\Delta ABC\) nhọn, kẻ đường cao $BD$ và $CE$ , vẽ các đường cao $DF$ và $EG$ của \(\Delta \;ADE\).
\(\Delta ABD\) đồng dạng với tam giác nào dưới đây?
Trả lời bởi giáo viên
Đáp án đúng: a
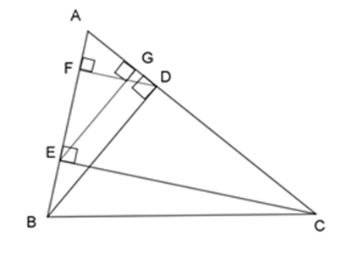
Xét \(\Delta ABD\) và $\Delta \;AEG$, ta có:
\(BD \bot AC\) ($BD$ là đường cao)
\(EG \bot AC\) ($EG$ là đường cao)
\( \Rightarrow BD{\rm{//}}EG\)
Theo định lý Talet, ta có:
\(\dfrac{{AE}}{{AB}} = \dfrac{{AG}}{{AD}} = \dfrac{{EG}}{{BD}}\)
\( \Rightarrow \)$\Delta AEG\backsim\Delta ABD$ (c - c -c) (điều phải chứng minh)
Hướng dẫn giải:
+ Áp dụng định lý Talet để tìm ra tỉ lệ thức của các cạnh tỉ lệ trong $2$ tam giác.
+ Từ đó suy ra 2 tam giác đồng dạng theo trường hợp cạnh – cạnh – cạnh.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
