Câu hỏi:
2 năm trước
Tứ giác \(ABCD\) có: \(AB = 9\,cm, BC = 20cm, CD = 25cm,\) \(AD = 12cm, BD = 15cm\).
Chọn câu sai.
Trả lời bởi giáo viên
Đáp án đúng: d
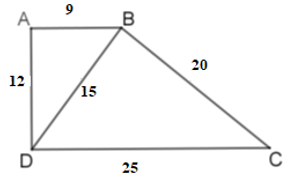
Ta có: \(\dfrac{{AB}}{{BD}} = \dfrac{{AD}}{{BC}} = \dfrac{{BD}}{{DC}}\) (vì \(\dfrac{9}{{15}} = \dfrac{{12}}{{20}} = \dfrac{{15}}{{25}}\,\left( { = \dfrac{3}{3}} \right)\)).
Suy ra \(\Delta ABD\backsim\Delta BDC\,\left( {c - c - c} \right)\)
\(\Delta ABD\backsim\Delta BDC\) nên \(\widehat {ABD} = \widehat {BDC}.\) Mà hai góc này ở vị trí so le trong nên \(AB\) //\(CD\). Vậy \(ABCD\) là hình thang.
Lại có: \(B{D^2} = 225 = A{D^2} + A{B^2}\) nên \(\Delta ABD\) vuông tại \(A\). Do đó \(ABCD\) là hình thang vuông.
Vậy A, B, C đều đúng, D sai.
Hướng dẫn giải:
+ Sử dụng cách chứng minh hai tam giác đồng dạng theo trường hợp cạnh-cạnh-cạnh.
+ Từ đó suy ra cặp góc tương ứng bằng nhau để chứng minh hai đường thẳng song song
+ Suy ra \(ABCD\) là hình thang.
Câu hỏi khác
- Bài tập định lý Ta-lét. Định lý đảo và hệ quả của định lý Ta-lét toán 8 có lời giải
- Bài tập tính chất đường phân giác của tam giác toán 8 có lời giải
- Bài tập hai tam giác đồng dạng toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ nhất toán 8 có lời giải
- Bài tập trường hợp đồng dạng thứ hai toán 8 có lời giải
