Cho tam giác\(ABC\). Các điểm \(D,E,F\) theo thứ tự là trung điểm của \(BC,CA,AB\). Các điểm \(A',B',C'\) theo thứ tự là trung điểm của \(EF,DF,DE\). Xét các khẳng định sau:

(I) \(\Delta EDF\backsim\Delta ABC\) theo tỉ số \(k = \dfrac{1}{2}\)                                   

(II) \(\Delta A'B'C'\backsim\Delta ABC\) theo tỉ số \(k = \dfrac{1}{4}\)                              

(III) \(\Delta A'B'C'\backsim\Delta EDF\) theo tỉ số \(k = 2\)

Số khẳng định đúng là:

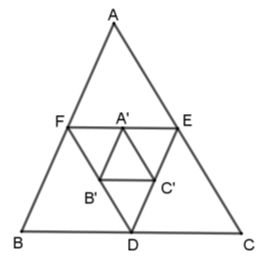
Vì \(D,E,F\) theo thứ tự là trung điểm của \(BC,CA,AB\) nên \(EF;\,ED;\,FD\) là các đường trung bình của tam giác \(ABC\) nên \(\dfrac{{EF}}{{BC}} = \dfrac{{FD}}{{AC}} = \dfrac{{ED}}{{AB}} = \dfrac{1}{2}\) suy ra \(\Delta EDF \backsim \Delta ABC\left( {c - c - c} \right)\) theo tỉ số đồng dạng \(k = \dfrac{1}{2}\) hay (I) đúng.

Tương tự ta có \(A'B';\,B'C';\,C'A'\) là các đường trung bình của tam giác \(DEF\) nên \(\Delta A'B'C'\backsim\Delta DEF\) theo tỉ số \(k = \dfrac{1}{2}\) nên (III) sai.

Theo tính chất đường trung bình \(\dfrac{{B'C'}}{{EF}} = \dfrac{1}{2}\) mà \(\dfrac{{EF}}{{BC}} = \dfrac{1}{2}\) (cmt) suy ra \(\dfrac{{B'C'}}{{BC}} = \dfrac{1}{4}.\)

Tương tự \(\dfrac{{A'B'}}{{AB}} = \dfrac{{A'C'}}{{AC}} = \dfrac{1}{4}.\)

Do đó \(\Delta A'B'C'\backsim\Delta ABC\,\left( {c - c - c} \right)\) theo tỉ số \(k = \dfrac{1}{4}\) hay (II) đúng.

Do đó có \(2\) khẳng định đúng.